xD:
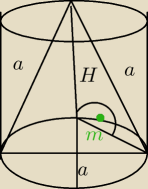
H − wysokość walca,
a − boki tego trójkąta i jednocześnie średnica podstawy
a2 − połowa średnicy, czyli promień podstawy
i tam jest kąt prosty (zielona kropka ^^
tutaj są wzory −−−>
1002
czyli tak pole podstawy możemy policzyć z wzoru na pole koła = πr
2 = π(
a2}
2 =
=
a24π = P
p
teraz jeszcze pole powierzchni bocznej = P
b. czyli potrzeba nam H i 2πr −−>
1002 (tak jak
to jest tutaj wytłumaczone)
mamy tam ten kąt prosty czyli możemy z twierdzenia Pitagorasa a
2=m
2(to na zielono) + H
2
H
2 = a
2 − m
2
tyle że nie mamy m. ale możemy go policzyć znowu z twierdzenia potagorasa
(
a2)
2 + (
a2)
2 = m
2 =
a24 +
a24 =
2a24 = m
2
i teraz H
H
2 = a
2 −
2a24 sprowadzamy do wspólnego mianowsnika czyli
H
2 =
4a24 −
2a24 =
2a24
i H =
√2a24 =
a√22.
mamy H trzeba nam jeszcze obwód koła, które jest podstawą (powierzchnia boczna to prostokąt o
bokach H i 2πr, czyli
2πr = 2 * π *
a2 = aπ
I liczymy pole boczne = 2πr * H = aπ *
a√22 =
a2√2π2
więc Pole całkowite = 2*P
p + P
b = 2 *
a24π +
a2√2π2 =
=
a2π2 +
a2√2π2 =
a2π√2 + a2π2 =
a2π(√2 + 1)2