Równanie prostej Anulka: Jakby to ktoś zadanie mógł rozwiązać: Są dane punkty A= ( −1, −2 ) B=(7,2) C = ( 1,4).Znajdź równanie prostej ,w której zawarta jest wysokość trójkąta ABC opuszczona z wierzchołka C i oblicz jego pole. Z góry dziękuje.

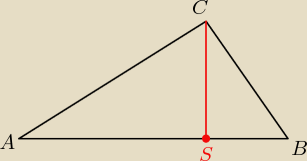
Trivial: 1. Wyznacz równanie prostej AB. 2. Zauważ, że prosta SC ⊥ prostej AB. 3. Wyznacz równanie prostej SC.

Trivial: Żeby obliczyć pole: 1. Oblicz |AB|. 2. Oblicz d(C, pr. AB) = h.

	1
3. P =		|AB|h.
	2

Paweł: Zadanie jest całkiem łatwe, napisze Ci jak je zrobic, a jeśli nadal nie będziesz wiedziała jak, to napisz jeszcze raz: Wiemy że wysokośc trójkąta jest to prosta prostopadła do prostej, w tym przypadku, AB. Wyznacz prostą AB. Następnie prosta przechodząca przez punkt C i prostopadła do prostej AB ( warunek prostopadłości − a1*a2=−1). Jest to nasza szukana wysokośc. Pole tego trójkąta wyliczysz ze wzoru P_{ABC}=1/2*|(x_B−x_A)(y_C−y_A)−(y_B−y_A)(x_C−x_A)| Powodzenia.

Gustlik: Są dane punkty A= ( −1, −2 ) B=(7,2) C = ( 1,4).Znajdź równanie prostej ,w której zawarta jest wysokość trójkąta ABC opuszczona z wierzchołka C i oblicz jego pole. Z góry dziękuje. Paweł, wzór na pole, który podałeś, wziął się z wyznacznika wektorów, tylko podałeś go w najbardziej pogmatwanej i mało "strawnej" wersji, szczerze mówiąc mimo iż mocno "siedzę" w matmie, to ten wzór musiałbym sobie każdorazowo wyprowadzać, albo zerżnąć z jakichś tablic czy opracowań, bo w tej wersji jest on trudny do zapamiętania, natomiast z wektorów zrobię to z marszu zbudzony w samym środku nocy, bo metoda jest łatwa i "wzrokowa". Pokażę łatwą do obliczania i zapamietania metodę − wyjaśnienie tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 1. Obliczam współrzędne wektorów AB^→ i AC^→ A=(−1, −2) B=(7,2) C = (1,4) AB^→=B−A=[7−(−1), 2−(−2)]=[8, 4] AC^→=C−A=[1−(−1), 4−(−2)]=[2, 6] Liczę wyznacznik tych wektorów: d(AB^→, AC^→)= | 8 4 | | 2 6 | =8*6−4*2=48−8=40

	1		1
Pole P=		|d(AB→, AC→)|=		*40=20
	2		2

Podobne zadanie masz tutaj 76292

Gustlik: Liczę r ównanie wysokości: 1) Obliczam współczynnik kierunkowy podstawy:

	yB−yA		7−(−1)		8
aAB=		=		=		=2
	xB−xA		2−(−2)		4

2) Wspólczynnik kierunkowy wysokości wyznaczam z warunku prostopadłości do podstawy AB:

	1		1
ah=−		=−
	aAB		2

Wysokość h ma równanie:

	1
y=−		x+b i przechodzi przez punkt C = (1,4)
	2

	1
4=−		*1+b
	2

	1
4=−		+b
	2

	1
4+		=b
	2

	1
b=4
	2

	1		1
Odp. Równanie wysokości: y=−		x+4
	2		2