[C[Proszę o pomoc - ekstrema i monotoniczność]] Student z plibudy: Proszę o pomoc − ekstrema i monotoniczność Wyznaczyć przedziały monotonicznośći i ekstrema lokalne funkcji f(x)=x²√4−x², x ∊ (−2,2) −−−−−−−−− o ile pochodną fukcji można obliczyć, to potem jest problem tego typu, że nie bardzo wiem jak to dokończyć, a jak coś mi wyjdzie, to wcale nie mieści się w tym przedziale

MathGym: jak porównujesz pochodną do zera to wychodzi równanie 2x − x³ = 0 i zero się mieści

MathGym: w równaniu zamiast 2 ma być 8

jo: Pochodna mi wyszła tyle

2x(4−x2)+x3
√4−x2

a z tego rozwiązania:

	2√6		2√6
x = −		x =		x = 0
	3		3

Jak dobrze obliczyłam bo się spieszę i na razie zmykam... Powodzenia!

marta: a mi inna pochodna wyszla

marta: mi wyszlo 8x−3x³

Student z plibudy: nie do końca wiem jak ty to zrobiłeś, a już na pewno nie wiem, jak mam z tego ekstrema obliczyć

Student z plibudy: ja jak liczyłem to normalnie mi wychodzi coś takiego:

	1
2x(4−x2)1/2 + x2*		(4−x2)−1/2 i to jest moja pochodne,
	2

ale to się różni od tego co wy zrobiliście troszkę

marta: tam powinno byc −x³ jak juz

marta: nie to to samo tyl ze bez przeksztalcen sprowadz to do wspolnego mianownika jakim jest ten pierwiastek i amsz postac ta co "jo"

marta: a nie bo Ty nie uwzgledniles pochodnej wewnetrzenj z funkcji pod pierwiastek

MathGym:

	1
f'(x) = (x2)'(√4 − x2 )+x2(√4 − x2 )' = 2x(√4 − x2 ) + x2		*(−2x)
	2√4 − x2 )

	−x3
= 2x(√4 − x2 ) +
	√4 − x2 )

Student z plibudy: hmm, a możesz to jakoś rozpisać, bo nie bardzo wiem jak on to przekształcił

MathGym: A więc −3x³ + 8x wychodzi

jo: Dobra ta pochodna, ja zgubiłam 'minus'.

Student z plibudy: aha, takie coś, ale czemu na końcu prz (−2x) mnożysz?

MathGym: właśnie podobnie jak ja na początku wynik 100% dobry

marta: bo to pochodna wewnetrzna z tego co masz pod pierwiastekiem

MathGym: def pochodnej złożonej pochodna funkcji zewnętrznej dla argumentu funkcji wewnętrznej razy pochodna funkcji wewnętrznej dlatego!

Student z plibudy: aa no tak [f(y)]' faktycznie to by miało sens już

Student z plibudy: no dobra, a co zrobić z tym jak już mi to −3x³ + 8x wyjdzie?

marta: z tego co pamietam to trzeba liczyc granice przy miejscach zerowych

Student z plibudy: hmm, ale nie łapie jeszcze jednego motywu, jeśli już wyjdzie taki ostateczny wynik, to brakuje mi pierwiastków, co sie znimi stało? bo skrócić się nie mogły, bo to dodawanie a nie mnożenie ...

MathGym: −3x³ + 8x = 0 −x(3x² − 8) = 0 i z tego liczysz pierwiastki

MathGym: malejąca jeżeli −x(3x² − 8) < 0 rosnaca −x(3x² − 8) > 0

MathGym: pierwiastki ktore wzsyz y tego to maks (3x&2 − 8) a w zerze min jasne juz wszystko

Student z plibudy: dobra to już prawie czaje, tylko nie bardzo wiem jak z tego:

	−x3
2x(√4 − x2 ) +
	√4 − x2

otzrzymałeś −3x³ + 8x?

Student z plibudy: i po co w ogóle w zadania jest podany przedział (−2,2) jeśli się z niego nie korzysta?

Student z plibudy: jak ktos się zna na tym, a widze, że problemów z tym nie macie, to podsyłam jeszcze kilka zadań, które będą prawdopodobnie na kolosie w piątek i musze to jakoś opanować, ale zadania przy okazji muszę oddać we wtorek zrobione do wykładowcy 73721

Student z plibudy: niby wyszło mi coś takiego:

8x−3x3*√4−x2
4−x2

ale nie czaje, gdzie u was podział się mianownik i pierwiastek z licznika?

marta: przeciez rozwiazujesz rownanie f'(x)=0 wiec mozemy przemnozyc przez mianownik bo on i tak nie moze sie rownac 0. Dlatego on znika

Student z plibudy: no dobra, a ten pierwiastek? a do czego są w ogóle te przedziały potrzebne, co są podane na początku zadania?

marta: no pierwiastek przeciez jest mianownikiem! aten przedzial to poprostu masz podane na jakim przedziale musisz rozpatrymac ekstrema

Student z plibudy: aaa czaje, to nie potzebnie usówałem niewymierność z mianownika, przez co ten pierwiatek przeszedł do licznika... hmm to już chyba czaję... wielkie thx za pomoc

tom: chyba przemnożył przez mianownik √4−x², całe rozwiązanie

marta: no dokladnie bardzo dobrze to sobie wytlumaczyles

Student z plibudy: więc czy wykres funkcji będzie wygladał w taki sposób? http://www.iv.pl/images/24558361769826472088.jpg czy też to zaczyna się rysować od prawej strony? bo już nie pamiętam. jeśli od prawej to na odwrót powinno być, a jeśli od lewej to jest dobrze. a i jeśli równanie będzie miało z przodu + to rysujemy od góry do dołu, a − to od dołu do góry?

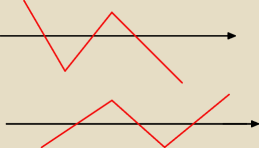
Student z plibudy: któryś z tych musi być poprawny, ale nie wiem który

jo: Jeżeli przy najwyższej potędze jest minus to od dołu jak plus to od góry... Czyli pierwszy dobrze.

Student z plibudy: ok thx

bloodi_girl: potrzebna mi pomoc, licze to zadanie po 100kroc i za kazdym razem wychodza mi pkt przegięcia x₁= − ²₃ x₂= ²₃ a powinno wyjść: pkt przegięcia x₁ = ^{2− √2} ₃ x₂ = ^{2+ √2} ₃ zadanie brzmi: znajdz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji: 5x² e^−3x + 7ln5 obliczylam juz II pochodna, po uproszczeniu wyglada ona tak: f''(x) = 5e^−3x (2−12x+9x²) nie mam pojęcia, co jest źle, bo za każdym razem mój wynik wygląda tak jak napisałam wyżej... błagam o pomoc

jo: Pochodna dobrze. Widocznie coś pomyliłaś rozwiązując równanie 9x²−12x+2=0.

jo: Za pomocą delty spokojnie rozwiąż to równanie i będzie dobrze

bloodi_girl: ale ja głupia ! dzięki wielkie... tak ostatnio na tych studiach mam mało do czynienia z trójmianem kwadratowym, że autentycznie na to nie wpadłam masakra <facepalm>