Nierówności z pierwiastkami Michał: Nierówności z pierwiastkami W jaki sposób rozwiązywać takie nierówności np. √x+1−√x−2≤1

mi: najpierw założenia x+1>0 i x−2>0 x>−1 i x>2 zatem część wspólna x>2

mi: teraz podnieś obustronnie do potęgi 2

Zielona Gałązka: "Mi" a nie czasem w założeniu znak ≥ 0? Michał jak słusznie pisze "Mi" podnieś obie strony do kwadratu ale pamiętaj, aby z lewej strony to był wzór skróconego mnożenia (a−b)². Składnik a² i b² zniweluje Ci pierwiastki lecz zostanie jeszcze z pierwiastkiem składnik 2ab, więc ponownie podniesiesz obie strony do kwadratu. Tylko składnik z pierwiastkiem zostaw sobie samotnie, jako jeden po lewej stronie a resztę przenieś na prawą.

mi: tak ≥

Michał: Tak zrobiłem... nurtuje mnie jednak pytanie czy mogę podnosić do kwadratu przy takiej nierówności

Basia: możesz, ale po przekształceniu do postaci √x+1≤1+√x−2 bo wtedy obie strony są nieujemne początkową też możesz, ale wymaga to już uzasadnienia oto ono: x+1>x−2 dla każdego x ⇒ √x+1>√x−2 dla każdego x ⇒ √x+1−√x−2>0 dla każdego x czyli obie strony nierówności są dodatnie i można podnieść obustronnie do kwadratu −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a ten warunek musi być spełniony, bo np. −9 <1 ale po obustronnym podniesieniu do kwadratu mamy sprzeczność 81<1 czyli np. z nierównością x−1<√x+1 już tak od razu nie można postąpić trzeba rozważyć 2 przypadki 1. x−1<0 i wtedy nierówność jest spełniona dla każdego x<1 bo x−1<0 a √x+1≥0 czyli x∊(−∞,1) i 2. x−1≥0 i dla x≥1 możesz podnieść do kwadratu x²−2x+1<x+1 x²−3x<0 x(x−3)<0 x∊(0,3) ale było x≥1 czyli x∊<1,3) zb.rozwiązań jest suma x∊[C[x∊(−∞,1)∪<1,3)=(−∞,3) a sprawdź co by wyszło gdybyś od razu podniósł do kwadratu

ja. : 5 − √2x < 3√2 − x

ja. : wytłumaczcie mi to , proszę. pilne .

monika290595: x√5+1<√6(3x+x)

Enclaar: Zadanie z nierówności z pierwiastkami Które z liczb całkowitych większych od −5 spełniają nierówność (√2 + 1)x > 2√2x − 1? Po rozwiązaniu tej nierówności wychodzi mi x − √2x + 1 > 0, a np. po podniesieniu do kwadratu tego równania wychodzi mi nierówność kwadratowa − x² +1 > 0 Jak sformulować odpowiedź ?

iteRacj@: (√2 + 1)x > 2√(2x) − 1 czy (√2 + 1)x > 2√2*x − 1 ?

Enclaar: Chodzi oczywiście o zadanie (√2 + 1)x > 2√2 *x − 1

Enclaar: Po rozwiązaniu tej nierówności wychodzi wyrażenie x − √2 x + 1 > 0.i oczywiście nie ma sensu podnosić do kwadratu, ale x to ułamek z liczbą niewymierną w mianowniku, a po jej usunięciu wychodzi mi x < −1 − √2. Wobec tego jakie liczby większe od −5 spełniają tę nierówność?

ite: (√2 + 1)x > 2√2 *x − 1 (√2 + 1)x − 2√2 *x >− 1 (√2 + 1 − 2√2)x >− 1 (1−√2)x >− 1

	−1
x<
	1−√2

	−(1+√2)
x<
	(1−√2)(1+√2)

x<1+√2 oraz x>−5 → x∊(−5; 1+√2)

Enclaar: Dziękuję bardzo!

Enclaar: Narysowano kąt ostry który ma miarę 30 stopni. Ramiona tego kąta przecięto prostą k i zaznaczono kąty alfa i beta tak, że miara kąta alfa stanowi 2/3 miary kąta beta. Jaka jest miara kąta alfa? A. 60 stopni, B. 75 sopni, C. 84 stopnie, D. 96 stopni.

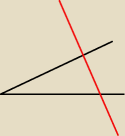
ABC: które to kąty? tam można na różne sposoby zaznaczać

PW:

	2
β+		β+30°=180°
	3

5
	β = 150°
3

β=90°

	2
α=		90°
	3

α=60° Zostaw już ten wątek sprzed prawie 10 lat. Jeżeli masz jakieś pytania − załóż nowy.

jc: f(x) = √x+1 − √x−2 ≤1, x≥2

	3
f jest funkcją malejącą, co widać, jak się inaczej zapisze wzór: f(x)=		,
	√x+1 + √x−2

f(3)=1, dlatego rozwiązaniami są liczby x nie mniejsze od 3.

Enclaar: Nie wiem jak ruszyć takie zadanie z kombinatoryki. Proszę o pomoc. W 7 −osobowym samochodzie mają zająć miejsca 3 osoby dorosłe i dwoje dzieci. Zakładamy że dzieci nie mogą zamować na 2 przednich siedzeniach. Na ile sposobów te osoby mogą zając miejsca w samochodzie?

iteRacj@: Czy ta ekipa wsiada do samochodu, żeby nim jechać , czyli na miejscu kierowcy ktoś musi siedzieć, najlepiej dorosły z prawem jazdy?

Enclaar: Tak, trzeba uwzględnić 1 osobę doroslą z prawem jazdy.

iteRacj@: 21:37 to nie rozumiem tego: każdy z nich może być kierowcą, czy tylko jedna osoba ma prawo jazdy?

Enclaar: tak

iteRacj@: Jedna osoba ma prawo jazdy → to rozwiązanie jest takie: a/ Na miejscu kierowcy siedzi jedyna osoba z prawem jazdy − 1 sposób, miejsce obok kierowcy jest puste, pozostałe dwie osoby dorosłe i dzieci siedzą losowo na czterech z pięciu miejsc z tyłu −

	5!
	(5−4)!

	5!
czyli 1*
	(5−4)!

b/ Na miejscu kierowcy siedzi jedyna osoba z prawem jazdy − 1 sposób, na miejscu obok kierowcy siedzi jedna z dwóch pozostałych osób dorosłych − 2 sposoby,

	5!
trzecia osoba dorosła i dzieci siedzą losowo na trzech z pięciu miejsc z tyłu −
	(5−3)!

	5!
czyli 1*2*
	(5−3)!

	5!		5!
ilość sposób zajęcia miejsc 1*		+1*2*
	(5−4)!		(5−3)!

Enclaar: Nie wiem czy dobrze liczę, ale z tego rachunku wychodzi mi 240, co chyba nie jest poprawne bo nie widzę 1 osoby przy kierownicy (1 sposób).

iteRacj@: W obu składnikach sumy początkowe mnożenie przez 1 to posadzenie jedynego kierowcy na miejscu za kierownicą. Czy to jest niejasne?

Enclaar: Wydaje mi się, że ten 1 sposób (osobę kierującą) trzeba dodać, a nie pomnożyć, ale może się mylę.

iteRacj@: Dla kierowcy trzeba zastosować regułę mnożenia. Może ktoś, kto jest nauczycielem, będzie chciał to wytłumaczyć profesjonalnie?

Jerzy: A co tutaj jest do tłumaczenia.Sadzamy za kierownicą osobę z prawem jazdy i traktujemy jakby jej nie było.Pozostałych uczestników rozmieszczamy na 6 miejscach.

Enclaar: Dziękuję za pomoc i pozdrawiam.

Enclaar: Czy zadania z kombinatoryki nie da się rozwiązać w jakiś prostszy sposób? Jest to zadanie z 8 klasy szkoły podstawowej, gdzie w programie nie ma pojęcia silni i wzoru Newtona.

Jerzy: Od kiedy rachunek prawdopodobieństwa jest w podstawówce ?

iteRacj@: Można to rozwiązanie zapisać bez silni i wzoru Newtona. a/ Na miejscu kierowcy siedzi jedyna osoba z prawem jazdy − 1 sposób, miejsce obok kierowcy jest puste, pozostają dwie osoby dorosłe i dwoje dzieci, które mają do wyboru na pięć miejsc z tyłu samochodu: pierwsza z ich ma do wyboru z 5 siedzeń, druga 4, trzecia 3 i ostatnia 2 czyli 1*5*4*3*2

iteRacj@: W podręcznikach do klasy ósmej jest kombinatoryka: http://flipbook.nowaera.pl/dokumenty/Flipbook/Matematyka-z-kluczem-podrecznik[kl_8][pr_2018][small]/?_ga=2.240335237.725551601.1558180553-1711610047.1558180553#p=5 lub https://flipbook.apps.gwo.pl/display/2444

Enclaar: Jak rozwiązać równanie wykładnicze typu; 2^2x2+4x+3 − 9*2^x2+2x+3 + 64 = 0 W tym wypadku nie wiem jak doprowadzić to równanie do wspólnej podstawy lub do wspólnego wykładnika.

Kamil18: 2x²+4x+3=(x+1)² +(x+1)² +1 x²+2x+3=(x+1)²+2

Jerzy: I teraz podstawienie: 2^{(x + 1)2} = t i warunek t > 0

Enclaar: Po podstawieniu wyszło mi rownanie: 4t² − 36t =0 ⇔ t(t−9) = 0 i t=0 i t=9 czy tak?

Jerzy: Hmm... raczej t powinno być potęgą o podstawie 2.Sprawdź jeszcze raz obliczenia i pokaż jakie masz równanie po podstawieniu t

Jerzy: 2t² − 36t + 64 = 0

Enclaar: Chyba to równanie kwadratowe nie jest poprawne, gdyż Δ = 68, a pierwiastki równania t są liczbami niewymiernymi.

ICSP: 2^{2x2 + 4x + 3} − 9^{x2 + 2x + 3} + 64 = 0 2^{2(x2 + 2x + 3)} * 2⁻³ − 92^{x2 + 2x + 3} + 64 = 0 2^{2(x2 + 2x + 3)} − 72*2^{x2 + 2x + 3} + 512 = 0 t = 2^{x2 + 2x + 3} t² − 72t + 512 = 0

Mirus: Mozecie pomóż z tym https://matematykaszkolna.pl/forum/399793.html

ICSP: chociaż z drugiej strony to świętej Δ liczyć nie umiesz. Δ = 784 = 26²

Jerzy: 784 = 28²

Jerzy: Δ = (−36)² − 4*2*64 = 784 √Δ = 28