geometria analityczna ona: Witam! Dane są dwie proste równoległe k:y+3x−1 oraz l: y=3x + 4. odlegość między tymi prostymi wynosi? Prosze i dziekuję...

toja: 0. dobrze podałaś treść zadania? 1. wziąć dowolny punkt na prostej np k (lub l) 2. napisać równie prostej prostopadłej do k przechodzącej przez wybrany punkt 3. Rozwiązać układ równań równanie otrzymanej prostej i prostej l otrzymasz współrzędne punktu przecięcia np B. 4. obliczyć odległość między wybranym i otrzymanym pkt

think: ona albo |k − l| = | y − 3x + 1 − y + 3x + 4 | = 5

think: wystarczy sprawdzić przesunięcie czyli wyraz wolny.

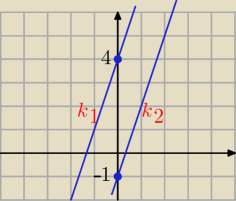
Bogdan: k₁: y = 3x + 4 ⇒ 3x − y + 4 = 0. k₂: y = 3x − 1 ⇒ 3x − y − 1 = 0 Bierzemy dowolny punkt należący do jednej z podanych prostych, np.: (0, 4) z prostej k−1. Obliczamy odległość d tego punktu do drugiej prostej, czyli do k₂ wg wzoru 1249.

	|3*0 + (−1)*4 − 1|		5
d =		=
	√3 + 1		√10

Można też zastosować gotowy wzór na odległość między prostymi równoległymi: k₁: y = a₁x + b₁ k₂: y = a₂x + b₂

	|b1 – b2|
d =
	√a2 + 1

toja: Hej! Think! Nie masz racji. odległość między prostymi równoległymi to: długość najkrótszego odcinka łączącego te proste. wektor przesunięcia nie musi być do nich prostopadły (a nawet nie jest!)