Matura rozszerzona z "Gazetą Wyborczą"
Ломоно́сов: Zadania z dzisiejszego arkusza maturalnego z matematyki, poziom rozszerzony, dołączonego do
"Gazety Wyborczej" :
1. 4 pkt
Rozwiąż równanie |x + 3| + |x + 1| = x + 18
2. 5 pkt
Wyznacz wszystkie wartości parametru m, dla których równanie x
2−mx+m−1 = 0 ma dwa różne
pierwiastki rzeczywiste x
1, x
2 spełniające warunek: |x
1 − x
2| > 2x
1 * 2x
2
3. 4 pkt
Wykaż, że jeżeli, x + y = 4 to x
3 + y
3 ≥ 16
4. 4 pkt
Ciąg (a,b,4) jest arytmetyczne, a ciąg (4,a,b) jest geometryczny. Oblicz a oraz b
5. 4 pkt
| | π | |
Wykaż, że jeżeli x ≠ |
| + 2kπ, gdzie k jest liczbą całkowitą, to |
| | 2 | |
| | π | | x | | cosx | |
tg( |
| + |
| ) = |
| |
| | 4 | | 2 | | 1 − sinx | |
6. 4 pkt
Prosta przechodząca przez środek jednego z boków trójkąta równobocznego i tworząca z tym bokiem
kąt ostry α dzieli ten trójkąt na czworokąt i trójkąt. Stosunek pola czworokąta do pola
trójkąta jest równy 5 : 3. Oblicz tangens kąta α
7. 6 pkt
W trapezie równoramiennym podstawy mają długości 9 i 12, a kąt między ramieniem trapezu i
dłuższą podstawą ma miarę 60 stopni. Oblicz promień okręgu opisanego na tym trapezie.
8. 5 pkt
Bok kwadratu opisanego na okręgu o równaniu x
2 + y
2 = 5 zawiera się w prostej o równaniu
x + 2y − 5 = 0. Oblicz współrzędne wierzchołków tego kwadratu.
9. 4 pkt
W prostopadłościanie długości krawędzi o wspólnym wierzchołku są równe a, b, c, długość
przekątnej prostopadłościanu jest równa d. Wykaż, że a + b + c ≤ d
√3
10. 5 pkt
Oblicz prawdopodobieństwo, że w pięciu rzutach symetryczną sześcienną kostką do gry suma
uzyskanych liczb oczek będzie równa 8.
11 paź 20:04
Godzio:
2.
x
2 − mx + m − 1 = 0
Δ > 0 ⇒ m
2 − 4m + 4 > 0 ⇒ (m − 2)
2 > 0 ⇒ m ≠ 2
|x
1 − x
2| > 2x
1x
2
√(x1 − x2)2 =
√(x1 + x2)2 − 4x1x2 > 2x
1x
2
√m2 − 4m + 4 > 2(m − 1)
√(m − 2)2 > 2(m − 1)
|m − 2| > 2m − 2
dla m ∊ (−
∞, 2)
−m + 2 > 2m − 2
−3m > −4
dla m ∊ (2,
∞)
m − 2 > 2m − 2
0 > m ⇒ m ∊ ∅
11 paź 20:09
Godzio:
Zadanie 3
x + y = 4 /3 ⇒ y = 4 − x
x3 + 3x2y + 3xy2 + y3 = 64
x3 + 3xy(x + y) + y3 = 64
x3 + 12xy + y3 = 64
x3 + y3 = 64 − 12xy
x3 + y3 ≥ 16
64 − 12xy ≥ 16
−12xy ≥ −48
xy ≤ 4
x(4 − x) ≤ 4
4x − x2 ≤ 4
x2 − 4x + 4 ≥ 0
(x − 2)2 ≥ 0
11 paź 20:18
Godzio:
Zadanie 4
a,b,4 −− arytmetyczny ⇒ 2b = a + 4
| | a2 | |
4,a,b −− geometryczny ⇒ a2 = 4b ⇒ b = |
| |
| | 4 | |
a
2 − 2a − 8 = 0
Δ = 4 + 32 = 36
√Δ = 6
| | 2 − 6 | |
a2 = |
| = −2 ⇒ b = 1 |
| | 2 | |
1) 4,4,4 lub −2,1,4
2) 4,4,4 lub 4,−2,1
11 paź 20:22
Godzio:
Zadanie 5
| | π | | x | | cosx | |
tg( |
| + |
| ) = |
| |
| | 4 | | 2 | | 1 − sinx | |
| | | cos(x/2) + sin(x/2) | |
| | | cos(x/2) | |
| |
= |
| = |
| | | cos(x/2) − sin(x/2) | |
| | | cos(x/2) | |
| |
| |
| = |
| | x | | x | | x | | x | | cos2 |
| − 2sinx |
| cos |
| + sin2 |
| | | | 2 | | 2 | | 2 | | 2 | |
| |
11 paź 20:31
Arni: Zad 3.
x3 + 3xy(x + y) + y3 = 64
czemu sie zrobilo potem 12?
11 paź 20:55
Godzio: bo x + y = 4
11 paź 21:00
Arni: a fakt.
Zad5.
4 zapis od gory, Dlaczego tak zamieniles jedynke? Nie moge sie doszukac wlasnosci zadnej ktora
by t ospelnila
11 paź 21:03
Godzio: sprowadziłem do wspólnego mianownika
11 paź 21:05
Arni: to fakt
zad5.
Drugi zapis , sam koniec, dlaczego tam powstal ulamek?
11 paź 21:11
Arni: to fakt
zad5.
Drugi zapis , sam koniec, dlaczego tam powstal ulamek?
11 paź 21:12
Godzio:
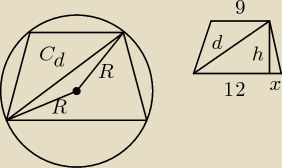 Zadanie 7
Zadanie 7
h
2 + 10,5
2 = d
2
d
2 = 117
d =
√117
Z tw. cos:
d
2 = 2R
2 − 2R
2cos120
| | 1 | |
117 = R2(2 − 2 * (− |
| ) ) |
| | 2 | |
117 = R
2 * 3
R
2 = 39
R =
√39
11 paź 21:15
Arni: i przy okazji zad 3;
xy ≤ 4
x(4 − x) ≤ 4
skad to drugie?
11 paź 21:15
Godzio:
| | x | | x | |
rozszerzyłem licznik i mianownik o cos |
| − sin |
| |
| | 2 | | 2 | |
11 paź 21:16
Godzio: na górze napisałem y = 4 − x
11 paź 21:16
Arni: chodzsi o 1+tgx2 / 1−tgx2
11 paź 21:22
Arni: jeju tepy jestem w porownaniu z toba

.
zad 7 pierwszy zapis , jest na to jakas regula ze podzieliles przez dwa?>
11 paź 21:23
Kejt: Godzio, zostaw coś dla innych

11 paź 21:27
Arni: tak przy okazji , masz jakies zestawienie wszyskich wlasciwosci i twierdzen abym mogl sie na
pamiec wyuczyc? moze wtedy latwiej mi to wszystkp pojdzie
11 paź 21:29
Godzio: To jest tak tylko przy trapezie równoramiennym po drugiej stronie jest taki sam x
więc:
| | 12 − 9 | |
12 − 2x = 9 => 12 − 9 = 2x => |
| = x |
| | 2 | |
Kejt w takim razie reszta dla Ciebie

11 paź 21:31
Godzio:
zestawiania własności nie mam bo raczej zapamiętuje z lekcji i później je utrwalam a trochę
tego jest

11 paź 21:34
Arni: d2 = 2R2 − 2R2cos120 a to skad?
11 paź 21:35
Kejt: nie, nie, naprawdę nie trzeba

zadowolę się 10.
11 paź 21:35
Godzio:
z twierdzenia cosinusów

Pomiędzy R i R jest kąt środkowy oparty na tym samym łuku co kąt 60
o więc ma miarę 120
o 
11 paź 21:40
Arni: a mozesz przytoczyc twierdzenie?
11 paź 21:47
Święty: Twierdzenie cosinusów jest na stronie
543
11 paź 21:54
Godzio:
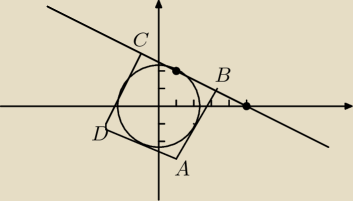 Zadanie 8
Zadanie 8
Z góry sorki za niedokładny rysunek

Punkt przecięcia okręgu do prostej to środek boku:
S
CB = (1,2)
środek okręgu: S(0,0)
| | 1 | | 1 | |
|SCBS| = |
| a = r ⇒ √5 = |
| a ⇒ a = 2√5 |
| | 2 | | 2 | |
| | 1 | |
|BS| = |
| a√2 i x + 2y − 5 = 0 |
| | 2 | |
B(x,y)
√x2 + y2 =
√10 /
2
x
2 + y
2 = 10 i x = 5 − 2y
25 − 20y + 5y
2 = 10
5y
2 − 20y + 15 = 0
y
2 − 4y + 3 = 0
(y − 3)(y − 1) = 0
y = 3 v y = 1
x = −1 v x = 3
B(3,1), C(−1,3)
| | 1 | | 5 | |
prosta prostpadła do y = − |
| x + |
| przechodząca przez B ma równanie: |
| | 2 | | 2 | |
y = 2x + b B(3,1)
1 = 6 + b
b = −5
y = 2x − 5
Długość |AB| = 2
√5 ⇒ (3 − x)
2 + (1 − y)
2 = 20
9 − 6x + x
2 + 4x
2 − 24x + 36 = 20
5x
2 − 30x + 25 = 0
x
2 − 6x + 5 = 0
(x − 5)(x − 1) = 0
x = 5 v x = 1
y = 5 v y = −3
A(1,−3) (drugi punkt jest po drugiej stronie ale on nas nie interesuje)
| | 1 | | 5 | |
Prosta równoległa do y = − |
| x + |
| przechodząca przez A: |
| | 2 | | 2 | |
b = −2,5
prosta CD:
y = 2x + b C(−1,3)
3 = −2 + b
b = 5
y = 2x + 5
punkt przeciecia tych prostych to punkt D :
2,5x = −7,5
x = −3
y = −1
D(−3,−1)
Odp:
A(1,−3), B(3,1), C(−1,3), D(−3,−1)
Mam nadzieję że bardzo na około nie zrobiłem

11 paź 21:59
Arni: |x1 − x2| > 2x1x2 a to z czego wynika?

Zad 2.
Jkaby ktos mial jakas strone ze wszystkimi wlasciwosciami , wzorami i twierdzeniami to prosze
zeby sie podzielil :<
11 paź 22:04
Godzio:
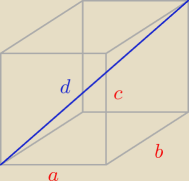 Zadanie 9
Zadanie 9
wiemy że:
d =
√c2 + a2 + b2
d2 = c2 + a2 + b2 ⇒ d
2 = (a + b + c)
2 − 2ab − 2ac − 2bc
d
2 + 2ab + 2ac + 2bc = (a + b + c)
2
a + b + c ≤ d
√3 /
2
(a + b + c)
2 ≤ 3d
2
d
2 + 2ab + 2ac + 2bc ≤ 3d
2
ab + ac + bc ≤
d2
ab + ac + bc ≤ c
2 + a
2 + b
2 /*2
a
2 − 2ab + b
2 + a
2 − 2ac + c
2 + b
2 − 2bc + c
2 ≥ 0
(a − b)
2 + (a − c)
2 + (b − c)
2 ≥ 0 c.n.d
11 paź 22:04
Godzio: Arni to wynika z polecenia

11 paź 22:05
Godzio:
Dobra to teraz zostało dla chętnych banalne zadanie 1,
do tego 6 i 10

11 paź 22:06
Arni: Ano tez prawda. A zapis ponizej?
11 paź 22:09
Godzio: A to trzeba już wpaść na pomysł jak to zapisać a jak wiadomo
√a2 = |a|
11 paź 22:09
Godzio:
Ломоно́сов, masz jakieś odpowiedzi żeby to posprawdzać?
11 paź 22:10
Arni: ok. tez juz czaje. a zapis ponizej?

11 paź 22:12
Kejt: 10 jest moje!

11 paź 22:12
Arni: a te wzore Veta czy jak mu bylo
11 paź 22:14
Godzio: zgadza sie

11 paź 22:16
Arni: dla m ∊ (−∞, 2) i ten drugi przedzial skad sie wzial?
11 paź 22:17
Ломоно́сов: Godzio, jedynie w zadaniu 8. , według szkicu rozwiązania w "Gazecie":
A=(3,1)
B=(−1,3)
C=(−3,−1)
D=(1,−3)
Reszta jest dobrze zrobiona
11 paź 22:17
Kejt:
zadanie 10
możliwości zdarzenia sprzyjającego:
1. 1 1 1 1 4
2. 1 1 2 3 1
3. 1 1 2 2 2
5+20+10=35
wszystkie możliwości:
|Ω|=n
k=6
5
powinnam to jeszcze dalej rozpisywać?
11 paź 22:19
Godzio:
Z tego co widzę to rozwiązanie w 8 jest ok tylko ja mam inne oznaczenia punktów ale ich
współrzędne są takie same jak u mnie

11 paź 22:25
Godzio: Jak na moje oko jest ok

, nigdy nie wiem kiedy używać tych permutacji bez powtórzeń
11 paź 22:29
Kejt: ale się teraz podbudowałam

11 paź 22:35
Godzio:
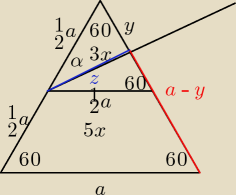 Zadanie 6
Zadanie 6
| | 3a2√3 | | 1 | |
P1 = 3x = |
| = |
| a*y*sin60 |
| | 32 | | 2 | |
| | 1 | | 1 | | 1 | | 3 | | 4a − 3a | | 1 | |
a − y − |
| a = |
| a − y = |
| a − |
| a = |
| = |
| a |
| | 2 | | 2 | | 2 | | 8 | | 8 | | 8 | |
z tw cos:
| | 1 | | 1 | | a2 | |
z2 = |
| a2 + |
| a2 − 2 * |
| * cos60 |
| | 4 | | 64 | | 32 | |
po skróceniu itd.
| | 15a2 | | √15a | |
z2 = |
| ⇒ z = |
| |
| | 64 | | 8 | |
Z tw. sinusuów:
| | y * sin60 | | | | 3√5 | |
sinα = |
| = |
| = |
| |
| | z | | √15a | | 10 | |
| | 55 | |
cos2α = 1 − sin2α = |
| |
| | 100 | |
| | sinα | | 3√5 | | 10 | | 3 | | 3√11 | |
tgα = |
| = |
| * |
| = |
| = |
| |
| | cosα | | 10 | | √55 | | √11 | | 11 | |
11 paź 22:39
mejciej: jak rozwiązywałeś zadanie nr.6 to musiałeś się gdzieś porządnie rąbnąć, ja zrobiłem metodą 3
razy
krótszą (mniejsza szansa na pomyłkę) i wyszło mi, że kąt alfa to pi/3. Przemyśl jeszcze raz
swoje rozwiązanie. Wskazówka: narysuj wysokość trójkąta, której spodkiem jest punk, w którym
nasza prosta przecina bok w połowie i względem wysokości odbij symetrycznie tą prostą.
Następnie zastosuj wzór na pole trójkąta bok*bok*sinus kąta między nimi*1/2. Wychodzi piękne
pi/3.
14 kwi 01:48
mejciej:
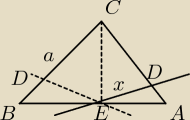
P
AED=
12*x*
a2*sin AED
oraz: P
EDCB=P
AED+2*
12*x*a*
√32*sin(
pi2−{AED}) oraz wiem, że:
sin(
pi2−{AED})=cos(AED); teraz to już tylko masz stosunek pól, niewiadome się skrócą,
sincos=tg

14 kwi 02:01
mejciej: sorry, tgα=3√3, a nie √3
14 kwi 14:47
cvb: mam pytanie do zadania 7 czemu kąt srodkowy ma miare 120 skoro lezy na przeciwko kata 120 , bo
kat przy podstawie ma 60 .
15 kwi 09:55
mejciej: generalnie to suma kątów przy ramieniu trapezu NA PŁASZCZYŹNIE jest równa π, w trójkącie NA
PŁASZCZYŹNIE też jest równa π. Jeżeli gdzieś wychodzi inaczej, to znaczy, że jest błąd...
Jeżeli będziesz się opierał na fundamentalnych twierdzeniach, to każde zadanie
rozwalisz raz − dwa. Wiem, sypię banałami, ale najtrudniej zawsze jest zauważyć
rzeczy oczywiste, one zazwyczaj prowadzą do najkrótszych rozwiązań

18 kwi 20:10
igor: mam pytanie do zadania 10 Kejt jak obliczyłaś poszczególne P1 P2 P3 z wariacji bez powtórzeń?
czy mogła byś to jakos jasniej rozpisac?
19 kwi 22:50
Kejt: ło jeny.. teraz?

to było tak dawno.. ja już nie pamiętam jak to robiłam

mogę Ci to
objaśnić jutro.. tylko musisz się przypomnieć.
19 kwi 22:52
;): |x
1 − x
2|
Godziu nawet nie musiałeś liczyć tego bo gdy a = 1 to zauważamy że
|x
1 − x
2| =
√Δ taki mały niuanse

Dopiero co wróciłem i za chwilkę również porobię te
zadanka
20 kwi 00:01
;): Nie zauważyłem a przecież to jest stare sam to nawet robiłem hehe

20 kwi 00:04
Aska: nie wie ktoś może, ile jest średnio zadań na maturze rozszerzonej?

20 kwi 00:19
Godzio: 11
20 kwi 00:20
;): 11 jest przeważnie chyba i 10
20 kwi 00:21
Basia:
Godziu
W zadaniu 8 posłużyłabym się wektorami
Po wyznaczeniu punktów B i C (tak jak zrobiłeś) masz
BS→=SD→
i
CS→SA→
A i D dostaniesz błyskawicznie
20 kwi 04:54
Basia:
Inny dowód
zadania 3
x+y = 4
(x+y)
3 = 4
3
x
3+3x
2y+3xy
2 + y
3 = 64
x
3+y
3 = 64 − 3x
2y−3xy
2
x
3+y
3 = 64 − 3xy(x+y)
x
3+y
3 = 64 − 12xy
x
3+y
3 = 64−12x(4−x)
x
3+y
3 = 12x
2−48x+64
x
3+y
3 = 4(3x
2−12x+16)
y = 3x
2−12x+16
Δ=(−12)
2−4*3*16 = 12*12−12*16 = 12(12−16) = −4*12 = −48
stąd
3x
2−12x+16≥4
stąd
x
3+y
3 ≥ 4*4=16
20 kwi 05:06
Basia:
niefortunnie użyta zmienna
nie y = 3x2−12x+16
tylko
f(x) = 3x2−12x+16
20 kwi 05:12
Basia:
Godziu
w zadaniu 4 masz wszystko dobrze oprócz odpowiedzi
a=4 i b=4
ciąg arytm. 4,4,4 i ciąg geometr. 4,4,4
lub
a= −2 i b=1
ciąg.arytm. −2,1,4 i ciąg geom. 4, −2, 1
20 kwi 06:10
Miłosz: Mam pytanie czy w zad 10 nie powinno być
5!3!*1!*2! 

21 kwi 12:59
Miłosz: Chodzi mi o to P2 obliczane przez kejt gdyż p1 i p3 mi pasuje a to nie bardzo
21 kwi 13:00
Sasza: czy ktoś obliczy zadanie 1?

21 kwi 17:22
Igor: Basia mam pytanie, czy ciąg stały jest ciągiem geometrycznym? Bo mnie uczono w szkole żeby tą
odpowiedź odrzucać. Jak to jest naprawdę?
27 kwi 18:57
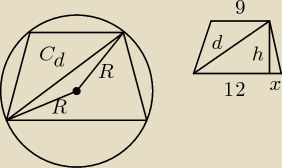 Zadanie 7
Zadanie 7
 .
zad 7 pierwszy zapis , jest na to jakas regula ze podzieliles przez dwa?>
.
zad 7 pierwszy zapis , jest na to jakas regula ze podzieliles przez dwa?>



 zadowolę się 10.
zadowolę się 10.
 Pomiędzy R i R jest kąt środkowy oparty na tym samym łuku co kąt 60o więc ma miarę 120o
Pomiędzy R i R jest kąt środkowy oparty na tym samym łuku co kąt 60o więc ma miarę 120o 
 Zadanie 8
Z góry sorki za niedokładny rysunek
Zadanie 8
Z góry sorki za niedokładny rysunek  Punkt przecięcia okręgu do prostej to środek boku:
SCB = (1,2)
środek okręgu: S(0,0)
Punkt przecięcia okręgu do prostej to środek boku:
SCB = (1,2)
środek okręgu: S(0,0)

 Zad 2.
Jkaby ktos mial jakas strone ze wszystkimi wlasciwosciami , wzorami i twierdzeniami to prosze
zeby sie podzielil :<
Zad 2.
Jkaby ktos mial jakas strone ze wszystkimi wlasciwosciami , wzorami i twierdzeniami to prosze
zeby sie podzielil :<
 Zadanie 9
wiemy że:
d = √c2 + a2 + b2
d2 = c2 + a2 + b2 ⇒ d2 = (a + b + c)2 − 2ab − 2ac − 2bc
d2 + 2ab + 2ac + 2bc = (a + b + c)2
a + b + c ≤ d√3 /2
(a + b + c)2 ≤ 3d2
d2 + 2ab + 2ac + 2bc ≤ 3d2
ab + ac + bc ≤ d2
ab + ac + bc ≤ c2 + a2 + b2 /*2
a2 − 2ab + b2 + a2 − 2ac + c2 + b2 − 2bc + c2 ≥ 0
(a − b)2 + (a − c)2 + (b − c)2 ≥ 0 c.n.d
Zadanie 9
wiemy że:
d = √c2 + a2 + b2
d2 = c2 + a2 + b2 ⇒ d2 = (a + b + c)2 − 2ab − 2ac − 2bc
d2 + 2ab + 2ac + 2bc = (a + b + c)2
a + b + c ≤ d√3 /2
(a + b + c)2 ≤ 3d2
d2 + 2ab + 2ac + 2bc ≤ 3d2
ab + ac + bc ≤ d2
ab + ac + bc ≤ c2 + a2 + b2 /*2
a2 − 2ab + b2 + a2 − 2ac + c2 + b2 − 2bc + c2 ≥ 0
(a − b)2 + (a − c)2 + (b − c)2 ≥ 0 c.n.d






 , nigdy nie wiem kiedy używać tych permutacji bez powtórzeń
, nigdy nie wiem kiedy używać tych permutacji bez powtórzeń

 Zadanie 6
Zadanie 6
 PAED=12*x*a2*sin AED
oraz: PEDCB=PAED+2*12*x*a*√32*sin(pi2−{AED}) oraz wiem, że:
sin(pi2−{AED})=cos(AED); teraz to już tylko masz stosunek pól, niewiadome się skrócą,
sincos=tg
PAED=12*x*a2*sin AED
oraz: PEDCB=PAED+2*12*x*a*√32*sin(pi2−{AED}) oraz wiem, że:
sin(pi2−{AED})=cos(AED); teraz to już tylko masz stosunek pól, niewiadome się skrócą,
sincos=tg 

 to było tak dawno.. ja już nie pamiętam jak to robiłam
to było tak dawno.. ja już nie pamiętam jak to robiłam  mogę Ci to
objaśnić jutro.. tylko musisz się przypomnieć.
mogę Ci to
objaśnić jutro.. tylko musisz się przypomnieć.
 Dopiero co wróciłem i za chwilkę również porobię te
zadanka
Dopiero co wróciłem i za chwilkę również porobię te
zadanka




