oblicz waska1989: Oblicz objętość graniastosłupa prawidłowego czworokątnego ,jeżeli przekątna ściany bocznej o dł. 20 cm tworzy z krawedzią podstawy kąt o mierze 60 stopni.

mila:

	√3
sin60=
	2

	h
sinα=
	p

√3		h
	=
2		20

	√3
2h=20
	2

	√3
h=10
	2

V=P_p*H P_P=a²

	a
cosα=
	p

	1
cos60=
	2

1		a
	=
2		20

2a=20 a=10

	√3
V=102*10
	2

V=100*5√3 V=500√3

mila: rysunek był i nie ma nie wiem co nie tak zrobiłam

mila:

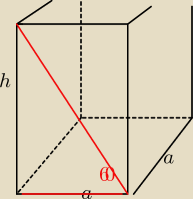
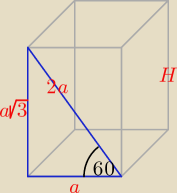Bogdan: Rozwiązanie powinno cechować się poprawnością, która obejmuje również rysunek. W graniastosłupie prawidłowym krawędzie dolnej i górnej podstawy leżą na równoległych płaszczyznach, ściany boczne są prostokątami, a nie np. trapezami. W tym zadaniu wykorzystujemy właściwości trójkąta prostokątnego o miarach kątów wewnętrznych: 30^o, 60^o, 90^o. Znajomość tego trójkąta jest wymagana już od uczniów gimnazjów 2280. 2a = 20 ⇒ a = 10 i wysokość H = 10√3, V = a³ √3 = 1000p[3}

miley: MILA W TYM MIEJSCU ZROBIŁAS BLĄD √3 2h=20 2 √3 h=10 2 DLATEGO WYMIK MASZ ZŁY! MI WYSZŁO TAK V = 1000 √3 POZDRAWIAM

miley: A NO I ZGADZAM SIĘ Z BOGDANEM, MOŻNA TO OBL. Z WŁASNOŚCI KATÓW TRÓJKĄTA PROSTOKĄTNEGO LUB JAK KTOŚ UMIE Z TRYGONOMETRII