5 paź 19:15
BenG: podbijam
5 paź 19:54
Jack:
wysil się...
5 paź 19:56
BenG: Nie siedzę z założonymi łapami i czekam na rozwiązanie, zrobiłem 6 ale nie wiem czy sposób jest
prawidłowy.
5 paź 20:03
BenG: podbijam
5 paź 20:28
BenG: podbijam...
5 paź 20:35
BenG: podbijam
5 paź 20:55
think: w pierwszym linku zadanie 6 z tą parabolą, wspólne punkty odczytuje się z wykresu
podpunkt b rozwiązuje się tak samo odczytując z wykresu g(x) ≤ 3 dla x≤3
podpunkt c, z wykresu odczytujesz dla jakich x−ów wykres prostej leży nad wykresem paraboli
5 paź 20:58
think: zad 8 (−1,0) ; (4,0); (0,−1)
wzór ogólny funkcji kwadratowej : ax
2 + bx + c
ale do tego skorzystamy z tego co wiemy P=(0,−1) ∊ y = a(x +1)(x − 4) ⇒ −1 = a*1*(−4) ⇒ a =
| | 1 | | 3 | |
więc wzór ogólny funkcji kwadratowej to: |
| x2 − |
| x − 1 |
| | 4 | | 4 | |
5 paź 21:02
think: eee to nie było 8 ale 7 sorki
5 paź 21:03
think: zad8 teraz
zbiór wartości <3,
∞) czyli a>0 i współrzędna y−kowa wierzchołka paraboli to q = 3 <−3,1>
przedział obustronnie domknięty czyli osią symetrii paraboli będzie x = −1 = p f(p) = q
f(−3) = 5
f(1) = 5
f(x) = ax
2 + bx + c
f(−3) = 9a − 3b + c = 5
f(1) = a + b + c = 5
oraz
f(−1) = a − b + c = 3
masz trzy równania z 3 niewiadomymi do rozwiązania.
5 paź 21:11
think: zad11
x
2 − x − 1 ≥ 0
Δ = 1 + 4 = 5
√Δ =
√5
największa całkowita ujemna to −1 a najmniejsza dodatnia to 2
5 paź 21:20
think:
z13
x + x + 4 + z = 48 ⇒ z = 44 − 2x
z to długość boku i nie może być ujemne, czyli 44 − 2x > 0 ⇒ x < 22
x
2 + (x + 4)
2 = z
2
x
2 + (x + 4)
2 = (44 − 2x)
2
rozwiąż równanie kwadratowe i pamiętaj o dziedzinie.
5 paź 21:23
5 paź 21:24
think: z14
x
2 − 2
√2x +1 = 0
| | 1 | | 1 | | x1 + x2 | |
masz policzyć |
| + |
| = |
| |
| | x1 | | x2 | | x1x2 | |
klasyk wzorów Vieta...
5 paź 21:24
think: z269 daruję sobie mam prawo
5 paź 21:25
think: z.289
r ⇒ P = πr2
r + 4 ⇒ Pz = π(r+ 4)2
Pz = 9P
π(r+ 4)2 = 9πr2
r2 + 8r + 16 = 9r2
rozwiąż równanie kwadratowe r >0 wyrażone w milimetrach...
5 paź 21:29
Eta:
zad. 8/ można rozwiązać prościej:
W( −1, 3)
z postaci kanonicznej
f(x) = a( x=1062 =3 i f(1)=5
to: 5= a( 1+1)
2+3 => 4a = 2 => a=
12
to: f(x) =
12( x +1)
2 +3 =
12( x
2+2x +1) +3
f(x) = 12x2 +x + 312
dla ......
5 paź 21:30
Eta:
poprawka chochlików
f(x) = a( x
+1)
2 +3
5 paź 21:32
BenG: wielkie dzięki think, już 2 raz tyłek mi ratujesz
mam do Ciebie takie pytanie, zastąpiłeś Jakuba?
5 paź 21:44
think: BenG zmartwię Cię
primo jestem babką secundo Jakub jest niezastąpiony i nie śmiałabym
5 paź 21:45
BenG: Przepraszam że zmieniłem Ci płeć
mimo to raz jeszcze dziękuję
5 paź 21:47
think: spoko loko póki sama nie zacznę jej zmieniać (w sensie płci)
miałeś prawo nie wiedzieć. No
proszę bardzo
5 paź 21:48
think: Etunia wcinam właśnie pokrojoną pigwę z cukrem, co przypomina Ciebie mi...
jutro będę
je obierać i zasypywać cukrem na sok do herbatki
5 paź 21:50
Eta:
Hehe
ja już zrobiłam nawet z niej ....
"nalewkę" .....
5 paź 21:52
think: nom też zrobiłam kilka lat temu i mam do tej pory
jakoś mało zużywamy tego typu specjałów,
łatwiej idzie produkcja niż konsumpcja...
5 paź 21:54
think: no to idę jeszcze z dwie pigwy skroić, bo tato mi podjadł a drugi raz mi się nie chce lecieć, w
końcu to taka nowalijka
pierwsza pigwunia w tym roku
5 paź 21:57
BenG: odnośnie pigwy to ja sączę zieloną herbatę z pigwą − polecam
5 paź 21:59
think: mogłabym się napić, o ile byłoby bez zielonej herbaty
nie przepadam za nią jak już coś to
wolę czerwoną.
5 paź 22:12
BenG: I <3 green tea
think, mam prośbę. Mogłabyś mi jaśniej przedstawić zadanie 7 i 8?
5 paź 22:17
think: zad 7 tam na rysunku, masz odczytać miejsca przecięcia wykresu z osiami współrzędnych są tam
między innymi miejsca zerowe paraboli
(−1,0) i (4,0)
korzystam z postaci iloczynowej
y = a(x − (−1))(x − 4)
i z rysunku odczytałam jeszcze punkt przecięcia z osią y−ek (0,−1)
więc podstawiam za x = 0 i y = −1 aby wyliczyć a i będę miała wzór funkcji kwadratowej.
−1 = a(0 + 1)(0 − 4) ⇒ a = ...
5 paź 22:27
BenG: aaaaa, no i teraz wszytko jasne, dzięki!
5 paź 22:33
think:
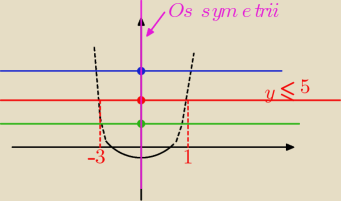
a z tym 8 to no niestety trzeba trochę zadanek z funkcji kwadratowej potrzaskać bo inaczej
ciężko będzie wyjaśnić coś takiego jak oczywistą oczywistość... jak na rysunku, że prowadząc
prostą równoległą do osi x to ona przecina i jej środek to oś symetrii, także bierze się
średnią liczb −3 i 1 i w ten sposób otrzymuję współrzędną wierzchołka paraboli. I jeszcze
kilka takich niuansów, no ale sorki nad tym trzeba usiąść i podumać, poszukać jakiś
właściwości, wyciągać wnioski a jeśli nie siedzisz nad matmą więcej niż to konieczne, to tak
jak nauczyć się angielskiego bez wkuwania słówek...
5 paź 22:36
think: raju zaczynam mętnie pisać więc pora urwać się spać, mam nadzieję, że Ci odrobinę wytłumaczyłam
o co biega a teraz spadam spać
5 paź 23:01
BenG: odrobinę? KOBIETO! Ty mi z nieba spadłaś!
5 paź 23:11
think: to dobrze, że przy tym Ci nie spadłam na głowę
bo trup na miejscu.
6 paź 07:56
https://matematykaszkolna.pl/forum/58860.html