Rozwiaż równanie Skizzo: I y I + y + I x I + x = 0

think: 1^o y >= 0 i x>=0 2y + 2x = 0 → y = − x a to wtedy i tylko wtedy gdy x = y = 0 bo oba mają być nieujemne 2^o y >= 0 x <= 0 2y − x + x = 0 → x e(−∞,0) i y = 0 3^o y <= 0 x >= 0 −y + y + 2x = 0 → ye(−∞,0) i x = 0 4^o y<=0 i x<= 0 −y + y − x + x = 0 zawsze.

Skizzo: dzieki

Skizzo: mam pytanie o co chodzi w tym pierwszym załozeniu moze mi ktos to wytłumaczyc

runny: y może być zarówno ujemny, jak i większy/równy zero x może być zarówno ujemny, jak i większy/równy zero Daje nam to cztery kombinacje, które kolejno rozpatrujemy.

Skizzo: → y = − x a to wtedy i tylko wtedy gdy x = y = 0 bo oba mają być nieujemne czyli co mniałbym tu zaznaczyc w układze wspołrzednych jesli oto by pytali w poleceniu 0 jesli tak to dlaczego

think: punkt (0,0)

runny: Dziedzina: x ∊ <0 ; ∞) Przeciwdziedzina: y ∊ <0; ∞) Skoro wykresem jest y = −x, to tylko jeden punkt tej prostej należy w tym samym czasie do dziedziny i przeciwdziedziny − będzie to punkt (0 ; 0)

think: a jaka inna liczba jest rozwiązaniem y = − x gdy obie te liczby mają być nie minusowe?

Skizzo: ale w załozeniach mamy x ∊ <0 ; ∞) i punkt (0,0) tu nalezy zastanawia mnie tylko ten −x

runny: Wykres prostej y = −x przechodzi przecież o punkt (0,0)

nie potrafie.. :( : think Skizzo: https://matematykaszkolna.pl/forum/58790.html wiecie z jakiego wzoru trzeba skorzystać i co podstawić

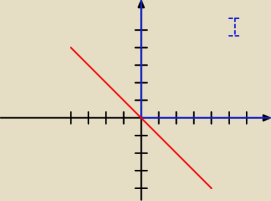
think: chodzi o pierwszy przypadek interesują nas rozwiązania z I ćwiartki układu współrzędnych włącznie z półosiami dodatnimi. Na rysunku zaznaczone na niebiesko. Na czerwono będzie wykres 2y + 2x = 0 / :2 y + x = 0 y = −x Rozwiązaniem jest część wspólna dla części niebieskiej i czerwonej.