Geometria - okręgi i proste. Kawaii: Bok rombu ma 10 cm, a jego dłuższa przekątna 16 cm. Oblicz promień okręgu wpisanego w ten romb.

M:

Min. Edukacji: https://matematykaszkolna.pl/strona/542.html

MS: przekątne rombu przecinają się pod kątem prostym i dzielą się dokładnie na połowę. Stąd też:

	d1		d2
a2 = (		)2 + (		)2
	2		2

po podstawieniu danych:

	16		d2
102 = (		)2 + (		)2
	2		2

d2=12 promień okręgu wpisanego to połowa wysokości rombu. Z porównania i przekształcenia wzorów na pole rombu:

	d1*d2
P =		= a * h = a * 2r
	2

	d1*d2		12*16		48		24
r =		=		=		=
	4*a		4*10		10		5

Mila: 4a²=e²+f² 4a²=16²+e² 400−256=e² e=12

	12*16
P=
	2

12*8=10*h

	48
h=2r=
	5

	24
r=
	5

=======

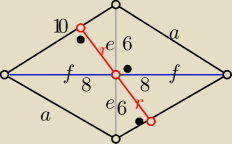
ala: Z tw. Pitagorasa : e= 6

	8*6
r=		= 4,8
	10