Panimetria Kamil: Tymek lezy w odległości 10m od drzewa widzi jego wierzchołek pod kątem 45^o.Drzewo ma wysokość: A)5m B)10m C)5√3 D)10√3

yyy: tg 45 x/10=tg45

Kamil: rysunek ktos pomoze prosze

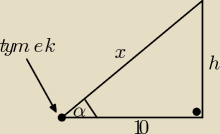
Święty: Na oko widać, że h=10, bo to połowa kwadratu o boku 10. Jeśli potrzebne obliczenia to... Do rozwiązania tego zadania niezbędna jest podstawowa wiedza z zakresu trygonometrii. https://matematykaszkolna.pl/strona/397.html Liczymy wartość x za pomocą cosinusa. Cos45=^√2₂ Układamy proporcję: ¹⁰_x=^√2₂ √2x=20 (mnożyliśmy na krzyż) x=²⁰_√2 Następnie możemy dalej korzystać z trygonometrii, bądz pozostały bok obliczyć ze sławnego twierdzenia Pitagorasa. 10²+h²=(²⁰_√2)² 100+h²=⁴⁰⁰₂ h=10

yyy:

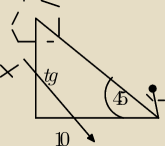
yyy: myślę że wyliczenie tego po prostu z tangensa jest łatwiejsze

Kamil: nie jestenm pewien czy dobrze zrozumiałem ze h=10, wytłumacz prosze

Spike: Niepotrzebnie komplikujecie sobie użyciem funkcji trygonometrycznych ( bądź co bądź podstawowych, ale zawsze) w tak prostym zadaniu. Skoro widzi drzewo pod kątem 45^o, a kąt między drzewem a podłożem ma 90^o, to siłą rzeczy trzeci kąt też ma 45^o. Z tego wynika, że jest to połowa kwadratu o boku długości wyrażonej jako odległość T. od drzewa. Więc h=10 Podstawowy rysunek wystarczy do rozwiązania tego zadania.

yyy: tak, tylko nie każdy to widzi.. Każdy ma różne sposoby na rozwiązywanie zadań. I aby komuś cos wytłumaczyc należy sie przystosowac i starać dopasować do jego toku myślenia.