godzio ! Lauraaa: Godzio zrobisz to te zadanie? Podstawy trapezu maja dlugosci 10 i 15 a ramiona sa rowne 6 i 8. Oblicz dlugosci przekatnych tego trapezu. Rozwiazuje sie tw cosinusow i ramiona tzreba oznaczyc jako x i y.. a co dalej ? moglabym prosic o rozwiazanie?

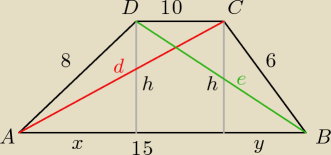
Godzio: x + y = 5 x² + h² = 8² y² + h² = 6² − −−−−−−−−−−−−−−−−−−−−−− x² − y² = 28 (x−y)(x+y) = 5 x = 5−y 5(5 − 2y) = 5 25 − 10y = 5 −10y = −20 y = 2 x = 3 h² + 4 = 36 h² = 32 h = 4√2 d² = (15−y)² + h² d² = 13² + 32 d² = 201 d = √201 e² = (15−x)² + h² e² = 12² + 32 e² = 176 e = 4√11 Zgadzają się odpowiedzi ?

Godzio: pomyliłem się, czekaj poprawka

Godzio: x² − y² = 28 x = 5−y 25 − 10y = 28 −10y = 3 y = −0,3 ?

robinka: https://matematykaszkolna.pl/forum/54249.html mnie też tyle wyszło

Godzio: no właśnie coś jest nie tak

robinka: coś jest nie tak z tym zadaniem kiedys już to zadanie robiłam i tak samo mi wyszło

Lauraaa: aha ok, w takim razie dziekuje. trudno nie bd zadania

Lauraaa: ale to np nie bd tak ze tworzymy uklad rownan tj x²= 6²+10²−2*6*10 cos α y²=6²+15²− 2*6*15*cos(180 stopni−α)

Godzio: to co Ci to da ?

Jack: wygląda na to że podane są sprzeczne dane, więc nie ma sensu czegokolwiek wyliczać.

Lauraaa: wtedy wyjdzie cosα= −x²+136/120 ?

Godzio: ale masz 2 równania i 3 niewiadome więc i tak nic Ci to nie da

Lauraaa: a to w sumie chyba macie racje, jutro na forum napisze co na to Pani Profesor dziekuje

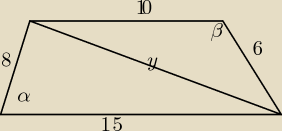
robinka: B=180−α cos(180−α)=−cosα y²=64+225−240cosα y²=36+100+120cosα 0=28+125−120cosα −153=−360cosα cos=0,425 a tak ?

robinka: ale coś jest nie tak

Lauraaa: a co dalej?

Lauraaa: ale dobrze, nie warto sie nurtowac tym zadaniem, jutro napisze na forum

Godzio: robinika do tego chyba potrzebna by była informacja że można opisać na nim koło

robinka: podstawiasz y²=64+225−240*0,425

robinka: masz racje Godzio

Jack: α i β to kąty naprzemianległe. Jest ok, jesli o to chodzi.

robinka: to nie są kąty naprzemianległe

Lauraaa: a nie bd y²=36+225−180stopni * (−cosα)

Jack: ok, racja , sorry − nie muszą dawać 180^o.

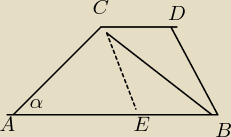
AS: Dane:AB = 15 , CD = 10 , AC = 8 , BD = 6 CE || BD ⇒ CE = BD = 6 , AE = AB − CD = 15 − 10 = 5 cos(α) obliczę z ΔACE (tw. cosinusów) CE² = AE² + BC² − 2*AE*AC

AS: dokończenie zadania przekątną BC znajduję z ΔABC majac dane AB,AC i cos (α) Podobnie postępuję z drugą przekątną. Poprawka CE² = AE² + AC² − 2*AC*AE*cos(α) (zacięła mi się grafika)

AS:

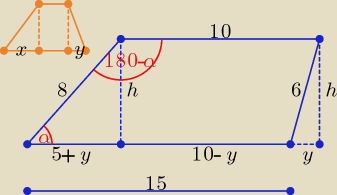
Bogdan: Jeśli w trapezie pomarańczowym y < 0 , to trapez ma kształt taki, jak narysowany tutaj linią niebieską. Dla wyznaczenia długości przekątnych tego trapezu można skorzystać z twierdzenia cosinusów.

	5 + y
cosα =
	8

cos(180^o − α) = −cosα Trzeba więc najpierw obliczyć wartość y, np. rozwiązując układ równań: h² + (5 + y)² = 64 h² + y² = 36

	3
Po odjęciu równań stronami otrzymujemy: 25 + 10y = 28 ⇒ y =
	10

	3   5 +   10		53
cosα =		=
	8		80

Za chwilę ciąg dalszy.

Bogdan:

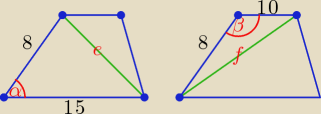
	53
e2 = 152 + 82 − 2*15*8*		⇒ e = ....
	80

	53
cosβ = cos(180 − α) = −cosα = −
	80

	53
f2 = 102 + 82 + 2*15*8*		⇒ f = ...
	80

robinka: teraz już wiem dlaczego wyszło mi −0,3 dzięki za rozwiązanie

Lauraaa: robilismy z Pania i wyszly ladne wyniki ale innym sposobem niz podany jest tutaj. wyszlo x²=225+36−180cos (−α) i y²=100+36−120 cosα i pozniej z tego wyliczalismy i w koncu wyszlo y=√120 lub y= √−130 i x= 3 √30 lub x= − 3 √30 przy zalozeniach y,x >0 odpowiedz: y=√120 i x= 3 p{30

AS: Przekątna BC = √130 (według mojego rysunku)

Lauraaa: aj aj dobrze 130