Na podstawie rysunku oblicz dokładną wartość sin 15 Samus: Na podstawie rysunku oblicz dokładną wartość sin 15 Oblicz dokładną wartość sin 75

b.: na początek przyjmij np. że pionowa przyprostokątna ma długość a, i powyliczaj na tej podstawie długości pozostałych boków −− próbuj... może się do tego przydać strona 397

b.: możesz zresztą równie dobrze przyjąć, że pionowa przyprostokątna ma długość 1...

Samus: Wciąż nie rozumiem, może ktoś pomóc?

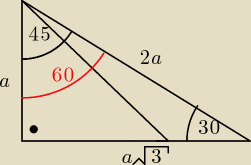
Kejt: teraz lepiej?

Samus: Wdzięczny jestem, że ktoś próbuje mi pomóc, ale dalej nic z mego rozumienia tego. Z tyłu ćwiczeń jest napisane że trzeba użyć wzoru P=ab sinα/2

	√2(√3−1)
Poprawny wynik:
	4

Nie wiem czemu, ale wychodzi gdy się obliczy pole biorąc sin30

	1		√2
P=		(√3−1)*1)/2*
	2		2

Ktoś mi może pomóc?

Samus: Poprawka

	1		{2}
P=		*(√3−1)*1*
	2		2

Kejt:

	√2
tam ma być		, tak?
	2

Samus: dokładnie

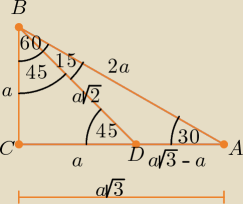
Bogdan: Oznaczamy: a = |BC| Korzystając z własności trójkątów prostokątnych o katach wewnętrznych mających miary: 30^o i 60^o oraz 45^o i 45^o otrzymujemy: |AC| = a√3, |AB| = 2a, |CD| = a, |BD| = a√2, |AD| = a√3 − a = a(√3 − 1)

	1		1
Pole trójkąta ABD: P =		* a(√3 − 1) * a =		a2(√3 − 1)
	2		2

	1		1
a także P =		* a√2 * 2a * sin15o =		a2 * 2√2sin15o
	2		2

	1		1
Stąd		a2(√3 − 1) =		a2 * 2√2sin15o ⇒ √3 − 1 = 2√2sin15o
	2		2

sin15^o = ... dokończ sam