Wytłumaczcie proszę! Równanie prostej. Martyna: Kilka zadań których kompletnie nie rozumiem i byłabym bardzo wdzięczna za pomoc! 1.napisz równanie prostej przechodzącej przez punkt a=(4,−3) i : a) równoległej do prostej 2x−3y+6=0 b)prostopadłej do prostej y=1/3x + 4 prost. −3x+b=y 2. napisz równanie prostej a)przechodzącej przez punkt a= (−3,5) i: b) równoległej do prostej y=2x−4 c)i prostopadłej do prostej 3x−2y−1=0 3.Napisz równanie prostej przechodzącej przez dwa dane punkty A(−−1,2) i B=(3, −2). ``

Gustlik: ad a) 2x−3y+6=0 −3y=−2x−6 /:(−3)

	2
y=		x+2
	3

Prosta rownoległa ma ten sam współczynnik kierunkowy:

	2
y=		x+b
	3

	2
−3=		*4+b
	3

	8
−3=		+b
	3

	2
−3−2		=b
	3

	2
b=−5
	3

Odp:

	2		2
y=		x−5
	3		3

Gustlik: ad b) y=1/3x + 4 Warunek prostopadłości:

	1
a2=−
	a1

Prosta prostopadła ma równanie: y=−3x+b a=(4,−3) −3=−3*4+b −3=−12+b −3+12=b 9=b b=9 Odp: y=−3x+9

Basia: ad.1a prosta równoległa do prostej 2x−3y+6=0 musi mieć równanie 2x−3y+C=0 przechodzi przez punkt A(4,−3) czyli współrzędne A muszą to równanie spełniać podstaw x=4, y=−3 wylicz C ad.b równanie już masz y=−3x+b podstaw za x i y jak w (a) policz b ad.2 identycznie ad.3 https://matematykaszkolna.pl/strona/1223.html

Gustlik: 2. napisz równanie prostej a)przechodzącej przez punkt a= (−3,5) i: b) równoległej do prostej y=2x−4 c)i prostopadłej do prostej 3x−2y−1=0 Równoległa: y=2x+b (ten sam wsp. kierunkowy) 5=2*(−3)+b → dokończ.... Prostopadła − najpierw przekształcam na postać kierunkową (funkcja liniowa): 3x−2y−1=0 −2y=−3x+1 /:(−2)

	3		1
y=		x−
	2		2

	1
Prostopadła ma równanie (a2=−		):
	a1

	2
y=−		x+b
	3

	2
5=−		*(−3)+b → dokończ....
	3

Robisz tak samo, jak poprzednie zadanie − a) i b).

Gustlik: ad 3) − podobne przykłady masz tutaj: 53894

Gustlik: Basiu − Ty znów kierujesz na stronę, gdzie jest mało "strawny" i trudny do zapamiętania wzór na prostą przechodzącą przez 2 punkty. Robi się tak: Wzór na wsp. kierunkowy

	yB−yA
a=
	xb−xA

następnie tak obliczony wsp. kierunkowy wstawia się do równania y=ax+b, potem wstawia sie współrzędne A lub B i wylicza b. Jest to prosta metoda i chyba dlatego nauczyciele unikają jej jak ognia, tak samo jak wzorów na równanie okręgu. Potrzebne są tylko DWA proste wzory:

	yB−yA
1) a=
	xb−xA

2) y=ax+b i żadnych układów równań, czy innych pokreconych wzorów. Po co mieszać uczniom w głowach? Na stronie 53894 jest wyjaśniony ten sposób wyznaczania równania prostej przechodzącej przez 2 punkty.

Basia: a ja robię i będę robić tak, bo takie są moje obyczaje

Eta:

Basia: Martyno napisz na podstawie wskazówek Gustlika równanie prostej przechodzącej przez A(1,5) i B(1,−1)

Gustlik: Basiu − jeszcze jedna sprawa: dla większości uczniów najłatwiejszą formą równania prostej jest postać kierunkowa y=ax+b − jest to po prostu funkcja liniowa. Dlatego jeżeli prosta jest podana innym równaniem, np. ogólnym, polecam przekształcenie na kierunkową − na niej najłatwiej rozwiązuje się większość zadań z równaniem prostej, a przede wszystkim najłatwiej ją z tego równania narysować na wykresie. Równanie ogólne jest natomiast bardziej przydatne do obliczania odległości punktu od prostej i tylko przy takich zadaniach polecam jego stosowanie.

Basia: chciałam nieśmiało zauważyć, że nie każda prosta jest wykresem funkcji liniowej

Gustlik: Basiu − wyjaśniam jeszcze raz: jeżeli w mianowniku wychodzi 0 − mamy prostą PIONOWĄ o równaniu x=c. Odczytujemy wówczas współrzędną x obu punktów i mamy równanie prostej. Zresztą widać to po takich samych współrzędnych x obu punktów. Jest to prosta x=1. Ty po prostu robisz jak każdy nauczyciel − jedziesz z Gdańska do Sopotu przez Paryż i Londyn zamiast prosto. Współczuję Twoim uczniom. Będą się męczyć na maturze i zabraknie im czasu na okrężne metody, bo tylko takie będą znali.

Gustlik: Prosta pionowa nie jest wykresem funkcji liniowej. Jej wyznaczanie wyjaśniłem w poście powyżej.

Godzio: przynajmniej jest śmiesznie "jedziesz z Gdańska do Sopotu przez Paryż i Londyn"

Nocny Mareczek: Chciałbym mieć takiego nauczyciela jak Gustlik − może w końcu bym się czegoś nauczył na lekcji.

Nocny Mareczek: Gustlik skąd jestes ? Udzielasz Korepetycji ?

Eta: Gustlik jeżeli już tak się upierasz przy tej metodzie, to pisz równanie prostej w takiej i tylko takiej postaci AB; ( y− y_A) )( x_A−x_B)= ( x−x_A)(y_A−y_B)

Basia: co to jest prosta pionowa ? moi "uczniowie" (pewnie by się obrazili za tę nazwę) raczej już mają matury za sobą teraz u mnie męczą się z aksjomatyczną teorią mnogości i teorią mocy, a u moich kolegów na analizie z całkami, które mają w mianowniku nierozkładalne trójmiany kwadratowe, bo mieli nauczycieli, którzy uważali, że lepiej parę wzorków na pamięć wyklepać niż nauczyć się myśleć przy zwijaniu trójmianu do postaci kanonicznej; wzorki zapomnieli, myśleć ich nie nauczono

Eta: Basiu Jedziesz ze mną na tę wycieczkę i Godzia też zabierzemy Zobaczymy Paryż i Londyn . Ludzie ...... szkoda zdrowia ...... jedźmy lepiej na wycieczkę

Łodzio: komu w droge temu czas

Godzio: No można by było pojechać, świata trochę zobaczyć

Nocny Marek:

Godzio: podoba mi się wczorajsza propozycja z Gdańska do Sopotu przez Nowy Jork

Basia: Z największą przyjemnością Eto ! Godzio jedziesz z nami ?

Godzio: No jak nie jak tak !

Basia: Ja bym wolała jakieś Karaiby, albo Wyspy Kanaryjskie, albo wyspy greckie. Te rejony gdzie dużo czystej i ciepłej wody. No i jakiś jachcik pełnomorski do tego.

Nocny Marek: Miłej podróży, niestety ja mam chorobę lokomocyjną

Gustlik: Eta, znam ten wzór, ale staram się go nie używać, jeżeli nie muszę, bo jest długi i trudny do zapamiętania i tylko zaśmieca uczniom głowę. Wielu osobom łatwo się pogubić z tymi współrzędnymi. Do Basi: chodzi o prostą x=c.− jest to prosta pionowa, równoległa do osi OY, natomiast prosta y=b (funkcja stała) to prosta pozioma równoległa do osi OX, a prosta y=ax+b to prosta ukośna. Są to jak najbardziej właściwe określenia. Z tego, co piszesz, zajmujesz się m.in. rachunkiem różniczkowym i całkowym. Na pewno znasz pojęcie np. asymptoty pionowej, poziomej i ukośnej. Co do zwijania trójmianu do postaci kanonicznej już pisałem:

	−b
p=
	2a

	−Δ
q=		lub q=f(p) i też nie jest potrzebna metoda "tu dodaj, tam odejmij".
	4a

Godzio: pomyślimy jutro ja już lecę spać Dobranoc

Nocny Marek: Dobranoc

Basia: A Godzio, jak widzę, najchętniej poszalałby na amerykańskich highwayach. Czemu nie, speeding to tylko przestępstwo stanowe, nie federalne. Nie damy się złapać.

Basia: Gustlik pionowa to jest u mnie rura w łazience. Nie istnieją proste pionowe, poziome ani ukośne. Są tylko równoległe, prostopadłe lub nachylone do osi OX pod kątem itd.

Eta: Basiu A w mojej łazience miała być pionowa ....... i "fachowcy" ją lekko "wygli"

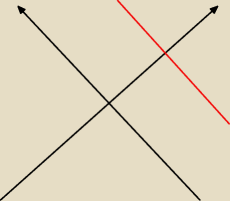
Basia: a to też jest układ równań; czy czerwona prosta jest pionowa ?

Basia: współrzędnych rzecz jasna

Eta: no..... ja widzę czerwoną prostopadłą do jednej z osi i zarazem równoległą do drugiej osi

Gustlik: Niech Ci będzie, że prosta równoległa do osi OY, jak już się tak upierasz. Ale zazwyczaj rysuje się układ tak, że oś OX leży poziomo, a oś OY pionowo, a więc prosta || do OY też leży wtedy pionowo. Uczniowie to wtedy dobrze rozumieją. Pozdrawiam

Basia: No i nie doczekam się niestety wyciągnięcia logicznych wniosków z dyskusji. Mnie chodzi o to, że ścisłość wymaga stwierdzenia:

	ya−yb
ponieważ xa≠xb mamy prawo napisać, że a =
	xa−xb

a jak nam się nie chce to już musimy posłużyć się wzorem podanym przez Etę. Układem równań też można się posłużyć tylko przy zastrzeżeniu, że x_a≠x_b

Eta: Witaj Basiu Jak tam? ...... emocje po wczorajszym już Cię opuściły ? U mnie upał jak ...........

Basia: Witaj Eto ! Chyba przestanę się przejmować. Skoro nikt się nie martwi o ścisłość zapisu to i ja nie muszę. Biedna tylko ta młodzież, od której potem na studiach wymagamy tej ścisłości, bo uważamy ją a całkowicie naturalną. U mnie też straszna kanikuła, ale wczoraj było jeszcze gorzej.

Gustlik: Basiu − przepraszam za "uczniów" myślałem, że jesteś nauczycielką w szkole średniej. Niemniej jednak jestem za pokazywaniem prostszych metod i dlatego tak robię, bo są przejrzyste dla uczniów. Powiem Ci coś: jeden z moich uczniów zastosował niedawno w szkole "moją" metodę przekształcania wzorami równania okręgu z postaci ogólnej na kanoniczną i dostał za to szóstkę! Mimo, iż tej metody w szkole nie miał, bo nauczycielka robiła to wzorami skróconego mnożenia. To jest jak najbardziej argument przemawiający za wprowadzeniem tej metody w szkole, jako alternatywnej. Dodam, że większość uczniów lepiej rozumie metodę "na wzory" niż szkolną metodę dopasowywania liczb pasujących do wzorów skróconego mnozenia. Ja te wzory oczywiście każdemu wyprowadzam, nie podaję ich "na ślepo", aby uczniowie wiedzieli, skąd się on e wzięły.

Martyna: Dziękuję wam bardzo robiłam tak jak pokazaliście, robiłam inne przykłady z podręcznika i odpowiedzi mi się zgadzały także naprawde jesteście genialni! tylko jedynie nie wiem co mam zrobić gdy mam rozwiązać równanie przechodzące przez 2 punkty jakoś mam to podstawiać? bo jak podstawie x i y to nic nie wychodzi. Ma ktoś pomysł?

Martyna: bo chodzi mi o to ze nie znam tej metody: ya−yb a = −−−−−−−−− xa−xb Pani w szkole nam takiej nie pokazywała ale mam nadzieje ze mi ją uzna