Nierówność wielomianowa (x^2-x-6)(x^2+2x+3)<0 Łukasz: Jak rozwiązać taką nierówność wielomianową (x²−x−6)(x²+2x+3)<0

Amaz: x∊(−2,3)? strzelam, bo w pamięci policzyłem

Edi: pomnożyć nawias przez nawias a potem poukladac i z schematu hornera doprowadzic do funkcji kwadratower, i potem wyliczyc delte i miejsca zerowe

Edi: 1401

ak1: Funkcja (x²−x−6)(x²+2x+3)<0 ⇔ gdy x²−x−6>0 ∧ x²+2x+3<0 lub x²−x−6<0 ∧ x²+2x+3>0 wyliczyć i zaznaczyć przedziały

Łukasz: Schematu hornera mnie w szkole nie uczyli na matmie wiec ta metoda odpada. a wynim −2 i 3 jest dobry tylko jak do tego dojsc. ak1 nie rozumiem co ja mam liczyc.

Łukasz: wymnozylem kazdy przez kazdy i po uporzadkowaniu otrzymalem X⁴+x³+x²−3x z tego wyciagnalem przed nawiaz x x(X³+x²+x−3) i podzielilem przez x−1 i delta wychodzi na minusie

Łukasz: Rozpisze mi ktoś ten przykład ?

Godzio: nie trzeba nic wymnażać w obu przykładach masz równanie kwadratowe z których liczysz pierwiastki zaraz powiem to zapisz

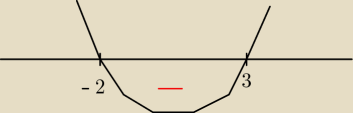
Godzio: (x² − x − 6)(x² + 2x + 3) < 0 liczysz w obu przypadkach Δ i pierwiastki: (x − 3)(x+2)(x² + 2x + 3) < 0 x² + 2x + 3 ≥ 0 bo a>0 i Δ<0 x = 3 v x = −2 szkicujesz sobie parabole zaznaczasz miejsca zerowe i odczytujesz rozwiązanie x ∊ (−2,3)

Godzio: poprawka: x² + 2x + 3 > 0 ...

Łukasz: jezeli wieksze od 0 to wynikiem nie bedzie przedzial −2 3

Godzio: tak, odpowiedź pozostaje bez zmian

min: 2x−3(x+2)=0

bezendu: 2x−3x−6=0 −x−6=0 −x=6 x=−6

Domcia1119: (x−4)²(x+2)(x+6)<0