dane są punkty A=-2,-3 i B=4,1 oraz prosta k o rownaniu 5x-2y+9=0 kapsell: dane są punkty A=−2,−3 i B=4,1 oraz prosta k o rownaniu 5x−2y+9=0 a) na prostej k znajdz punkt C rowno oddalony od punktow A i b b) Oblicz pole trojkata ABC prosilbym o pomoc

kalafiorowa: a) https://matematykaszkolna.pl/strona/1249.html b) skorzystaj ze wzoru na dlugosc odcinka oraz z wzoru Herona

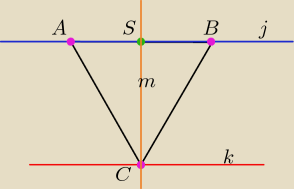
Testoviron: kalafiorowa − moze i taka metoda tez bylaby dobra, ale ja pokaze jak mozna to zrobic innym sposobem zalaczam rysunek pomocniczy Co wiemy(dane): A=(−2,−3) B=(4,1) przez punkt C przechodzi prosta k o rownaniu 5x−2y+9=0 Teraz przejde do zadania

	xa+xb		ya+yb
Obliczam srodek odcinka |AB| ze wzoru S=(		,		)
	2		2

S=(1,−1) Nastepnie obliczam rownanie prostej przechodzacej przez 2 punkty (A i B) wzor: (y−y_a)(x_b−x_a)−(y_b−y_a)(x−x_a)=0 (y+3)(4+2)−(1+3)(x+2)=0 4y+2y+12+6−x−2−3x−6=0 nastepnie to porzadkujemy i wychodzi 6y−4x+10=0 y na lewo i reszta na prawo abysmy mogli zapisac rownanie prostej y=ax+b 6y=4x−10 /6

	4		10
y=		−
	6		6

skracamy

	2		5
y=		−
	3		3

i mamy rownanie prostej przechodzacej przez punkt A i B (prosta j na rysunku)

	2		5
nastepnie szukamy prostej prostopadlej do prostej y=		−
	3		3

prosta prostopadla to jest odwrotnosc ze zmiana znaku liczby a w funkcji y=ax+b

	2		2		5
czyli w tym wypadku jest to liczba		to prosta prostopadla do funkcji y=		−
	3		3		3

bedzie prosta (m na rysunku) y=−{3}{2}x+b teraz wykorzystamy srodek odcinka |AB| czyli punkt S=(1,−1) (x=1 y=−1) i podstawiamy do prostej prostopadlej y=−{3}{2}x+b

	3
−1=−		*1+b
	2

1
	=b
2

	1
majac punkt b mozna dokonczyc rownanie prostej prostopadlej czyli da nam to y=−{3}{2}x+
	2

Teraz majac prosta m i prosta k mozna wyliczyc punkt C robiac uklad rownan

	1
y=−{3}{2}x+		/*2
	2

5x−2y+9=0 2y=−3x+1 −2y=−5x−9 −−−−−−−−−−−−−−− −8x−8=0 −8x=8/(−8) x=−1 <−−−− punkt x od wspolzednej punktu C teraz podstawiam x pod jedno z rownan −2y=−5(−1)−9 −2y=5−9 −2y=−4/(−2) y=2 <−−−− punkt y od wspolzednej punktu C tak wiec C=(−1,2) aby obliczyc pole trojkata nie musimy obliczac dlugosci bokow, wystarczy skorzystac ze wzroru:

	1
PΔABC=		|(xb−xa)(yc−ya)−(yb−ya)(xc−xa)|
	2

podstawiamy punkty pod wzór

	1
PΔABC=		|(4+2)(2+3)−(4+3)(−1+2)|
	2

	1
PΔABC=		|(6)(5)−(7)(1)|
	2

	1
PΔABC=		|30−7|
	2

	1
PΔABC=11		j2
	2

Karla: Jest błąd −1= ³₂ * 1 + b nie równa się jak napisałeś b=¹₂ tylko −1 − 1,5 = b ⇔ b= − 2,5

Ajtek:

	3
Nie ma błędu, zauważ że: y=−		x+b
	2

czyli:

	3		1
−1=−		*1+b →		=b
	2		2

Krl:

	5		9
A jak napiszę, że punkt C jest postaci (c,		c+		)
	2		2

i postawie warunek: |AC|=|BC| Bo tak próbuje i mi nie chce wyjść

Krl: Ktoś wie?

Kingaaaaaa: też robiłąm twoim sposobem Krl i mi nie wychodziło, jakieś cudaczne liczby.......... dlatego tu zajrzałam właśnie. Ale uważam że to bardzo dobry i sprytny sposób, dlaczego nie chce wyjść

Rol: Może dlatego, ze rysunek pomocniczy jest zły? k nie jest równoległe do odcinka AB

Siti: Właśnie liczę to zadanie i przy dobrze wykonanym rysunku od razu widać, jaki to ma być punkt. Próbowałam liczyć ze wzoru na odległość punktu od prostej, ale w końcu dorysowałam prostą l prostopadłą do prostej m, w której zawiera się odcinek AB.Po wyliczeniu wzorów tych prostych przyrównałam prostą l do prostej k i wynik wyszedł C(−1,2). Rysunek potwierdza to.

kubkins: w równaniu pola jest błąd, powinno być P= |(4+2)(2+3)+(1+3)(−1+2)| = 17

kubkins: w równaniu pola jest błąd, powinno być P= |(4+2)(2+3)−(1+3)(−1+2)| = 17

UnLow: Jak dla mnie to winno być tak: Punkt C (−1, 2) |AC|=|BC|=√1²+5²=√26 |AB|=√6²+4²=2√13 h=|SC|

	1
|AS|=		|AB|=√13
	2

h²=|AC|²−|AS|² h²=26−13 h=√13

	1
PΔABC=		|AB|*h
	2

	1
PΔABC=		*2*√13*√13
	2

P_ΔABC=13