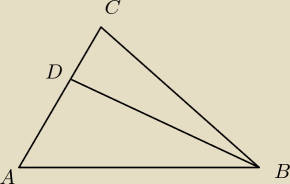
 w trójkącie ABc dane są kąt ABC = 60 stopni i |AB|=√31. Na boku AC obrano taki punkt D, że
długość odcinka AD wynosi 3. Znajdź długość BC jeśli |BD|=2√7
w trójkącie ABc dane są kąt ABC = 60 stopni i |AB|=√31. Na boku AC obrano taki punkt D, że
długość odcinka AD wynosi 3. Znajdź długość BC jeśli |BD|=2√7
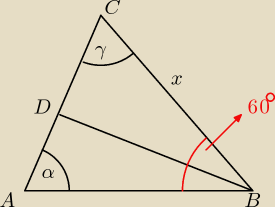 543 dla ABD |BD|2 = |AD|2 + |AB|2 −2|AD|*|AB|*cosα 28=9+31−6√31cosα
543 dla ABD |BD|2 = |AD|2 + |AB|2 −2|AD|*|AB|*cosα 28=9+31−6√31cosα
| 2 | 3√3 | |||
cosα= | sinα = √1−(2/√31)2= | α+γ=120o (bo ∑ kątów | ||
| √31 | √31 |
| √3 | 2 | 1 | √3 | 5√3 | ||||||
* | + | * | = | |||||||
| 2 | √31 | 2 | √31 | 2√31 |
| |AB| | x | √31*3*√31 | x√31 | |||||
549 dla ΔABC : | = | ; | = | → | ||||
| sinγ | sinα | 5√3 | 3√3 |
| 9 | ||
x = | √31 | |
| 5 |