 mam takie zadanie i nie umiem go do końca rozpracować:
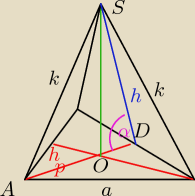
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest 2 razy większe od pola jego
podstawy. Oblicz miarę kąta nachylenia ściany bocznej do płaszczyzny podstawy.
mam takie zadanie i nie umiem go do końca rozpracować:
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest 2 razy większe od pola jego
podstawy. Oblicz miarę kąta nachylenia ściany bocznej do płaszczyzny podstawy.
| a2√3 | a√3 | |||
pole podstawy Pp= | hp= | |||
| 4 | 2 |
| 1 | a2√3 | a√3 | ||||
pole pow. bocznej Pb=3* | ha=2* | →h= | ||||
| 2 | 4 | 3 |
| 1 | a√3 | |OD| | a√3 | 3 | 1 | |||||||
|OD|= | hp= | sinα= | = | * | = | α=60o | ||||||
| 3 | 6 | h | 6 | a√3 | 2 |




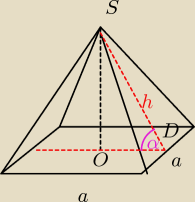
| a | a | 1 | ||||
Pp = a2 Pb=4 * | h = 2a2 →h=a zΔSDO cosα= | : a = | α=60o | |||
| 2 | 2 | 2 |
