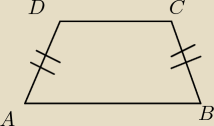
geometria analityczna - wektory Madzia: Trapez jest równoramienny. Muszę obliczyć współrzędne wierzchołka D jeśli: A(0,−5) ; B(4,3) ; C(−1,3). Jest to zadanie z działu geometria analityczna − wektory.

Jack: Policz wektor CB. Wektor AD będzie bardzo podobny do CB, ale będzie się różnił znakiem przy współrzędnej "Δx" (nachylenie ramion jest takie samo ale w przeciwną stronę). Następnie do punktu A dodaj wektor AD. Otrzymasz punkt D.

Jack: Będzie wygodniej liczyć wektor [BC], niż [CB].

Madzia: Próbowałam liczyć długość [AD] i [BC] i porównywać, ale mam wtedy dwie niewiadome, a'propos współrzędnej "Δx" nie miałam jej na lekcji i nie za bardzo wiem jak ją obliczyć. Czy wiesz może czy jest prostszy sposób na rozwiązanie tego zadania? p.s. Dzięki, że chcesz mi pomóc!

mique: Madzia, a co oznaczają te dwie rownolegle na AD i BC?

Jack: na pewno ją miałaś, jeśli miałaś wektory Zerknij tu https://matematykaszkolna.pl/strona/1623.html

Jack: jeśli [BC]=|−1−4, 3−3|=|−5,0|, to [AD]=[5,0] "Δx" to po prostu różnica x−ów punktów Teraz do puntu A dodaj ten wektor [AD]

Jack: odwołuje, tak się tego nie zrobi. Teraz zobaczyłem że ten rysunek niewiele odpowiada rzeczywistości zadania

Jack: idź za wskazówką mique.

Madzia: Mique te dwie kreski oznaczają, że boki są równej miary.

Madzia: Wiem, że rysunek jest "trochę" mylny... Sorki

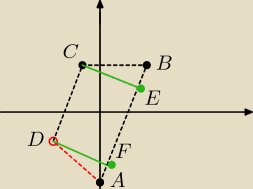
Jack: 1. Wyznacz równanie prostej przechodzącej przez A i B. 2. Wyznacz równianie prostej przechodzącej przez C i D (równoległa do 1) przechodząca przez punkt C) 3. Oblicz odległość punktu C od prostej z 1). 4. z Tw. Pit policz dł. odcinka |EB|. 5. Zrób wektor [EB]. 6. Wektor [EB] dodaj do punktu A. Dostaniesz punkt F. 7. Stwórz prostej prostopadłej do tej 1) przechodzącej przez punkt F. 8. Oblicz punkt przecięcia 2) i tej przed chwilą stworzonej.

Madzia: Wielkie dzięki

Jack: proszę (musiałem to zrobić bo na początku wprowadziłem Cię w błąd ).