Wielościany i bryły obrotowe mario_166: Witam, mam prośbę mógłby mi ktoś pomóc w rozwiązaniu tych zadanian bo z tych działów to jestem cieniutki (wielościany i bryły obrotowe), bardzo proszę o rozwiązanie w miarę możliwości, z góry dziękuje. 1. Suma długości krawędzi dwóch sześcianów równa się 12 dm, a suma ich objętości 468 dm³. Znajdź długość krawędzi tych sześcianów. 2. W ostrosłupie prawidłowym czworokątnym o polu podstawy 36 cm², kąt nachylenia krawędzi bocznej do płaszczyzny podstawy równy jest 60 stopni. Oblicz objętość i pole powierzchni bocznej ostrosłupa. 3. Oblicz pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość równą 8, a długość wysokości ostrosłupa jest równa 6. 4. Objętość ostrosłupa prawidłowego sześciokątnego jest równa 3000√3cm². Oblicz wysokość ostrosłupa wiedząc, że jest ona dwa razy większa od krawędzi podstawy. 5. Wysokość walca jest o 2 cm dłuższa od średnicy postawy, natomiast przekątna przekroju osiowego jest o 7 cm dłuższa od promienia podstawy. Oblicz objętość i pole powierzchni całkowitej walca. 6. Przekątna przekroju osiowego walca ma długość równą 10 cm. Stosunek promienia podstawy walca do jego wysokości wynosi ³₈. Oblicz objętość i pole powierzchni całkowitej walca. 7. Oblicz objętość i pole powierzchni bocznej walca, który powstał przez obrót prostokąta dookoła dłuższego boku wiedząc, że pole tego prostokąta jest równe 135 cm², a stosunek długości boków jest równy 3:5. 8. Oblicz objętość i pole powierzchni całkowitej stożka, mając dany jego promień r=4 cm i tworzącą l=5 cm. 9. Oblicz objętość i pole powierzchni całkowitej stożka, o tworzącej długości 4 i kącie rozwarcia o mierze 60 stopni. 10. Objętość stożka jest równa 12 π cm³, a pole jego podstawy 9πcm². Oblicz pole przekroju osiowego.

mario_166: odświeżam

mario_166: odświeżam

mario_166: odświeżam

Jack: próbowałeś któreś z tych zadań robić?

mario_166: coś tam próbowałem, ale z matmy jestem cieniutki i nie chcę żeby było źle

Jack: spróbuj tu to ostatnie rozwiązać, ok?

mario_166: za bardzo nie dam rady bo nie umiem

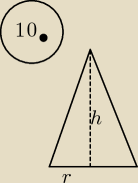
tom: 10. P_p = 9π = πr² stąd r = 3

	1		1
V= 12π =		hPp więc 12π=		h*9π stąd h= 4
	3		3

szukane pole P = rh = 12 wzory są na 1003 560 503

mario_166: wielkie dzięki, a dałbyś radę rozwiązać jeszcze pozostałe ?

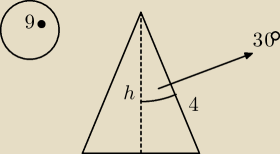
tom: przrekrój osiowy tego stożka jest trójkątem równobocznym o boku 4, więc

	4√3
r=2 h=		= 2√3
	2

	1		1		8√3π
V =		h* πr2 =		2√3π22 =
	3		3		3

P_c=πr(r+l) = π*2*(2+4)= 12π

mario_166: odświeżam

mario_166: odświeżam

mario_166: odświeżam

mario_166: odświeżam