okrąg ania: Czy mógłby ktoś mi wytłumaczyć jak to zrobić? okrąg o środku w punkcie S=(−1,2) i promieniu r=2 ma dwa punkty wspólne z prostą AB,gdy: A=(−3,4) B=(1,4) A=(−2,5) B=(−2,−1) A=(−3,3) B=(0,0)

tom: okrąg ma 2 punkty wspólne z prostą ⇔ gdy odległość prostej od środka okręgu jest mniejsza od promienia tu1249 znajdziesz wzór na odl. prostej od punktu, policz i porównaj

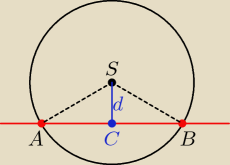
Eta: odległość d środka S od prostej musi być : d<r 1) sposób: A(−3,4) B( 1,4) i d < 2 punkt C jest środkiem odcinka AB to:

	xA+xB		yA+yB
xC=		.... i yC=
	2		2

x_C= −1 i y_C= 4 C( −1,4) wyznaczamy: d=ISCI = √(x_C−x_S)²+(y_C−y_S)²= √0+4= 2 d=2=r więc prosta AB jest styczna , czyli ma jeden punkt wspólny z tym okręgiem podobnie policz dla pozostałych przypadków i podaj właściwą odp

ania: Dziękuję bardzo gdy :A=(−2,5) B=(−2,−1) ,bo d=1,więc d<r,bo 1<2

ania: Eto ,a mogłabyś mi to sprawdzić i jeszcze pomóc? https://matematykaszkolna.pl/forum/42051.html