Najmniejszą i najwieksza wartość :) : Wyznaczyć wartość najmniejszą i największą funkcji f na zbiorze D. f(x,y)= y² − x² D={(x,y)∊R² : x² + y²≤25, y≥3}

wredulus_pospolitus: 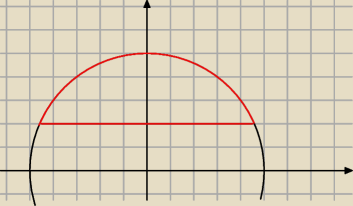czerwony to brzeg obszaru. I albo robimy całą zabawę jak chociażby tutaj Ci pokazałem: https://matematykaszkolna.pl/forum/421149.html Albo jesteśmy 'szprytni' i sobie ułatwiamy sprawę: 1. Największa wartość: niech y = conts. f_MAX(x,y) = f(0,y) czyli dla wybranego 'y' wartość funkcji f(x,y) zależy tylko od 'x' ... a ze względu jak wygląda funkcja f(x,y) to im mniejsza wartość |x| tym większa wartość funkcji Więc już wiemy, że największa wartość będzie postaci f(0,y) = f(y) = y² − 0 = y² ; y∊[3,5] Stąd mamy: f_MAX = f(0,5) = 25 2. Najmniejsza wartość: niech x = conts. f_MIN(x,y) = f(x,3) czyli dla wybranego 'x' wartość funkcji f(x,y) zależy tylko od 'y' ... a ze względu jak wygląda funkcja f(x,y) (i obszar) to im mniejsza wartość 'y' tym mniejsza wartość funkcji Więc już wiemy, że najmniejsza wartość będzie postaci f(x,3) = 3² − x = 9−x² ; x∊[−5,5] Stąd mamy: f_MIN = f(−5,3) = f(5,3) = 9 − 25 = −14

wredulus_pospolitus: źle zaznaczyłem obszar ... ale same rozumowanie pozostaje bez zmian

Student: ale f(5,3)∉D , linia czerwona pozioma jest y = 2 , a powinno być y =3

Student: f_MIN(4,3) = −5 , f_MAX(0,5) = 25

Student: f '(x) = −2x f '(y) = 2y ⇒P(0;0)∉D ,tworzymy funkcję na brzegu obszaru D ; x² + y² = 25 ⇒y² = 25 −x² , f(x) = 25−2x² , ⇒ f '(x) = −4x , f '(x) =0 ⇔x=0 , y = 5 lub y = −5

;): skąd wziąłeś te punkty przy wyznaczaniu wartości minimalnej? Czemu to 4, a nie jakaś liczba trochę ponad 4?

Student: badałem na krańca obszaru D, bo na liniach brzegowych , y =3 , oraz y = √25 −x² wychodzi f '(x) = 0 ⇔x=0 , a wewnątrz obszaru D nie ma punkt dla ekstremum patrz kryteria z Hesjanem !

wredulus_pospolitus: robiłem w pośpiechu i BŁĘDNIE podałem : x∊[−5;5] −−−> winno być x∊[−4 ; 4]

;): aaa już widzę, bardzo dziękuję wam za pomoc.

;): mam jeszcze problem z tym przykładem: f(x,y)=x²+2y²−2xy−2y D={(x,y)∊R² : x²/2 ≤ y ≤2} Jakbyście mieli chwilkę, żeby zerknąć to byłabym bardzo wdzięczna.

wredulus_pospolitus: zauważ, że f(x,y) = x² − 2xy + y² + y² − 2y + 1 − 1 = (x−y)² + (y−1)² − 1 i znowu ... możesz robić całą procedurę ... sprawdzać ekstrema lokalne wewnątrz obszaru ... a następnie sprawdzać ekstrema na brzegach. Albo możesz spróbować maksymalizować / minimalizować wartość patrząc na tą postać funkcji. Minimalna wartość: 1. chcemy aby (y−1)² = 0 −−−> y = 1 ... chcemy aby (x−y)² = (x−1)² = 0 −−−> x = 1 więc dla punktu (1,1) będziemy mieli minimalną wartość funkcji: f(1,1) = 0 + 0 − 1 = −1 Maksymalna wartość:

	x2
1. chcemy zmaksymalizować wartość wyrażenia (y−1)2 ... jako, że		≥ 0 (czyli wiemy, że
	2

na pewno y≥0) to mamy dwie możliwości: I. y = 2 −−−> (y−1)² = 1 −−−> maksymalizujemy (x−2)² ... co będzie miało miejsce dla x = −2 stąd mamy punkt (−2 , 2) co daje nam f(−2,2) = (−4)² + 1² − 1 = 16

	x2
II y =		= 0 ... czyli x = 0 ale to daje nam f(0,0) = 0 + 1 − 1 = 0 co daje
	2

mniejszą wartość ... więc odrzucamy ten przypadek.

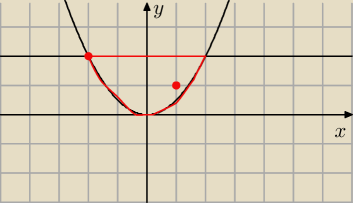
wredulus_pospolitus: A jakbyś chciała zrobić całą procedurę ... warto sobie najpierw narysować obszar D I jak widzisz ... tym razem wyszło nam że jeden z punktów (minimalny) będzie wewnątrz obszaru D ... a nie na jego brzegu.

wredulus_pospolitus: Zalecam Ci jednak przerobić całą procedurę ... dlaczego ... dlatego, że: 1. przy innym przykładzie możesz nie zauważyć jak zapisać funkcję, abyś mogła w łatwy sposób wykonać dedukcję , 2. możesz dokonać błędnej dedukcji, 3. możesz otrzymać taką funkcję w której powyższa dedukcja może być o wiele bardziej skomplikowana.

:) : Dobra czyli punkt z warunku koniecznego : (1,1) i on należy do dziedziny. Potem badam y=2 dla x∊(−2,2) I wychodzi P(2,2) nie należy do dziedziny Potem y=x²/2 dla xe(−2,2) I wyszły mi punkty P(0,0) ∊D P(2,2) nie należy I pitem sprawdzam wartości dla tych punktów co mi wyszły+ punktów na tych skrajnych punktach i wyszło mi wartość minimalna dla (1,1), a wartość maksymalna dla (−2,2). W podręczniku punkt w którym funkcja osiąga maksimum to (2,−2). Wiesz gdzie zrobiłam błąd?

. : Błąd jest w książce. Punkt (2, − 2) nie należy do przedziału D. Komus się kopnelo gdzie minusa dać.