liczby zespolone Student: z = ( 1− √2 j )⁴ , obliczyć ⁴√z

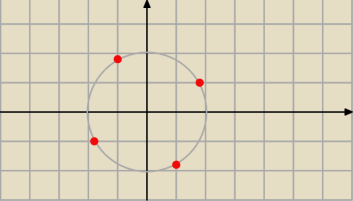
wredulus_pospolitus: fizyku .... jeden pierwiastek znasz od razu: 1 − √2j drugi to przemnożenie przez (−1) czyli −1 + √2j pozostałe dwa będą obrotem o 90^o względem punktu (0,0) czyli √2 + j oraz −√2 − j to było: jak sobie z tym poradzić gdy mamy PROSTY przykład i nie potrzebujemy robić obliczeń ... a ważny jest jedynie rezultat (plus −−− gdybyś to dobrze opisał, to byś zapunktował u prowadzącego) Standardowa droga: 1. v = 1 + √2j 2. zapisujemy w postaci trygonometrycznej: |v| =√1² + (√2)² = √3 więc v = √3(cosα + jsinα)

	1		−√2
innymi słowy: cosα =		; sinα =		(zostawiamy w tej postaci)
	√3		√3

UWAGA Możemy próbować 'wyłuskać' z tablic wartość kąta α, ale jest to zbyteczne 3. z = v⁴ −−−> ze wzoru de Moivier'a −−> z = v⁴ = (√3)⁴(cos(4α) + jsin(4α)) 4. Pierwiastkowanie:

	4α + 2kπ		4α + 2kπ
w = 4√z4 = 4√(√3)4(cos		+ jsin		) =
	4		4

	kπ		kπ
= √3(cos(α +		) + jsin(α +		) gdzie k∊{0,1,2,3}
	2		2

i stąd mamy: w₁ = √3(cosα + jsinα) = v = 1 − √2j w₂ = √3(cos(α + ^π/₂) + jsin(α + ^π/₂)) = // stosujemy wiedzę ze szkoły średniej // = = √3(−sinα + jcosα) = √2 + j w₃ = √3(cos(α + π) + jsin(α + π)) = // stosujemy wiedzę ze szkoły średniej // = = √3(−cosα − jsinα) = −1 + √2j w₄ = √3(cos(α + ^3π/₂) + jsin(α + ^3π/₂)) = // stosujemy wiedzę ze szkoły średniej // = = √3(sinα − jcosα) = −√2 − j I masz te cztery pierwiastki (jak widzisz −−− obyło się bez wyznaczania kąta)

wredulus_pospolitus: wiedza ze szkoły średniej: https://matematykaszkolna.pl/strona/431.html

Leszek: ten pierwszy sposób jest lepszy ! mamy pierwiastek głowny : w₁= 1 − √2 j , każdy następny jest obrócony o argument Δα = 2π/n , w tym przypadku Δα = π/2 czyli w₂ = (1−√2 j)*(cos π/2 + j sin π/2 ) = √2 +j w₃ = (1− √2 j)*(cos π + j sin π ) = −1 + √2 j w₄ = (1− √2 j) *( cos 3π/2 + j sin 3π/2 ) = √2 − j zauważ , że w₁ + w₂ + w₃ + w₄ = 0

Leszek: pomyłkca druku : powinnobyć : w₄ = − √2 − j

wredulus_pospolitus: @ Leszek −−− oczywiście, że jest lepszy ... a ile obrót mamy o wartość będącą wielokrotnością 360^o ale już policzenie ⁷√1 − √2j w ten sposób to już tragedia nawet ⁹√1 − √2j w ten sposób zbyt przyjemny nie będzie

Leszek: zgadzam się z Kolegą całkowicie !

Leszek: jak dają do rozwiązania "dziwolongi" typu z= √5 + √7j i obliczyć ⁵√z to tylko numerycznie z kalkulatorem !