czy da sie wykonac to zadanie bez twierdzen,jedynie tales , pola i podobienstwo? stasta: Dany jest trójkąt ABC. Na bokach AC i BC tego trójkąta leżą odpowiednio punkty L i K. Odcinki AK i BL przecinają się w takim punkcie M, ze pola trójkątów AMB, KLM i KMB są równe odpowiednio 144, 12 oraz 36. Oblicz pole trójkąta ABC.

Mila: Da się, dość prosto. Do jutra

X: Podobne https://matematykaszkolna.pl/forum/399725.html

M:

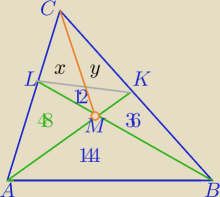
Mila: 1)

LM		12		1
	=		=		− Δ o takiej samej wysokości.⇒
MB		36		3

	1
PAMB=		*144=48
	3

2) P_LMC=x, P_KMC=y W Δ CLB:

x		LM		x		1
	=		⇔		=		⇔
y+36		MB		y+36		3

3x=y+36⇔y=3x−36 3) W ΔAKC:

x+48		144		x+48
	=		⇔		=4
y		36		y

4y=x+48 4) 4*(3x−36)=x+48 12x−144=x+48 11x=192

	192
x=
	11

	192		180
y=3*		−36=U{576−396}=
	11		11

	372		9
x+y=		=33+
	11		11

5)

	9
PΔABC=48+144+36+33+
	11

	9		2880
PΔABC=261		=
	11		11

=================== Sprawdzaj rachunki

Mila: II sposób: reguła wyprowadzona przez jednego Pana Matematyka, znajdziesz w internecie.

1		1		1		1
	+		=		+
Δ		144		144+48		144+36

Mila: chichi pokazał jeszcze inny sposób, może tu spojrzy

chichi: sposobów innych jest dużo. nie wiem, o który Ci chodzi @Milu?

Mila: Też nie pamiętam, ale był krótki Pozdrawiam, jak sesja, już są zerówki?

chichi: sesja zaczyna się za cirka 2tyg. mam jeden egzamin ustny i już tylko obrona magisterki

Mila: O rany, jak ten czas leci, już magisterka! Powodzenia i gratuluję terminowego ukończenia studiów.

chichi: dziękuję, wszystkiego dobrego i dużo zdrówka

Mila:

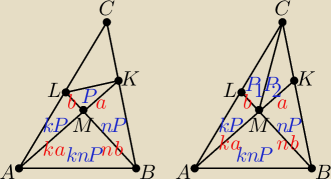
Bogdan: Zostałem tutaj zacytowany, korzystam więc z tej okazji i wracam do tematu. Długości: |MK| = a, |AM| = ka, |ML| = b, |BM| = nb, Pola: P_LMK=P, P_AML=kP, P_BMK=nP, P_ABM =knP, P_LMC=P₁, P_MKC=P₂ Rozwiązanie zadania:

	k(n+1)		n(k+1)
kP+P1=kP2 i nP+P2=nP1 ⇒ P1=		i P2=
	kn−1		kn−1

	kn(k+1)(n+1)
Pole trójkąta ABC: PABC=P1+P2+kP+nP+knP ⇒ PABC =		P
	kn−1

	4*3*5*4		2880
W podanym zadaniu jest k=4 i n=3 i P=12: PABC=		*12=
	4*3−1		11

Dodatkowo:

	(k+1)(n+1)		5*4		240
PLKC=		=		*12 =
	kn−1		11		11

P_ABKL=(k+1)(n+1)P = 5*4*12=240 Jeśli k = n to czworokąt ABKL jest trapezem i wtedy P_ABKL=(k+1)²P

Mila:

Mila: Ładny wzór na pole ΔABC. Właśnie o to pytałam chichi.

Mila:

	k*(n+1)
P1=		*P
	nk−1

	n(k+1)
P2=		*P
	nk−1

Bogdan:

	(k+1)(n+1)
Chochlik połknął P jeszcze w jednym miejscu, uzupełniam: PLKC =		P.
	kn−1

Dziękuję Mila i pozdrawiam

Mila: