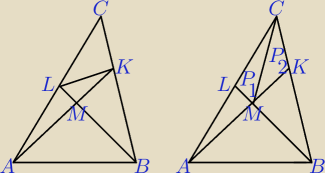
 Pola trójkątów:
PKMB = 52 i PKLM = 26 ⇒ |BM| = 2|LM|
PAMB = 364 i PKLM = 26 ⇒ |AM| = 7|MK|
2PAML = 364 ⇒ PAML = 182
PLMC = P1 i PMKC = P2
2P1 = P2 + 52 i 7P2 = P1 + 182 ⇒ P1 = 42 i P2 = 32
Pole PABC = 182 + 364 + 52 + 42 + 32 = 672
Pola trójkątów:
PKMB = 52 i PKLM = 26 ⇒ |BM| = 2|LM|
PAMB = 364 i PKLM = 26 ⇒ |AM| = 7|MK|
2PAML = 364 ⇒ PAML = 182
PLMC = P1 i PMKC = P2
2P1 = P2 + 52 i 7P2 = P1 + 182 ⇒ P1 = 42 i P2 = 32
Pole PABC = 182 + 364 + 52 + 42 + 32 = 672
 A jeszcze mam pytanko, dlaczego w tym przypadku jak liczymy stosunek długości boków,
a mamy podane Pola, których skala jest podniesiona do kwadratu, to czy stosunek boków nie
powinien być pomnożony przez kwadrat skali?
A jeszcze mam pytanko, dlaczego w tym przypadku jak liczymy stosunek długości boków,
a mamy podane Pola, których skala jest podniesiona do kwadratu, to czy stosunek boków nie
powinien być pomnożony przez kwadrat skali?
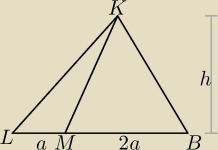 W zadaniu nie ma podobnych trójkątów.
W zadaniu nie ma podobnych trójkątów.
| 1 | 1 | |||
PKLM = | ah i PKMB = | *2ah ⇒ PKMB = 2PKLM | ||
| 2 | 2 |