dowod geometryczny
matematycznyswir:

W trójkącie ABC kąt ABC jest ostry i ma miarę dwa razy większą od miary α kąta BAC. Punkt D
jest punktem boku AB i β oznacza miarę kąta ostrego BDC.
Wykaż, że jeżeli sin2α = tgβ to BD = AD + BC
Utknąłem na tym, że BC=DE i dalej nie wiem jak to pociągnąć.
1 mar 20:44
palacz:
Wierzchołki (punkty) oznaczamy dużymi literami
1 mar 21:35
Iryt:
Poczekaj chwilę

1 mar 21:54
1 mar 22:16
matematycznyswir: Mój błąd, rysunek robiłem w pośpiechu − stąd brak wielkich liter. Nic to jednak nie zmienia w
treści zadania.
Co do podobnego zadania − kojarzę je z grudniowej matury próbnej i próbowałem analogicznie coś
tutaj wymyślić, ale bezskutecznie. Czy ktoś mógłby mi wyjaśnić jak to doprowadzić do końca w
wersji dla opornych?
2 mar 17:48
wredulus_pospolitus:
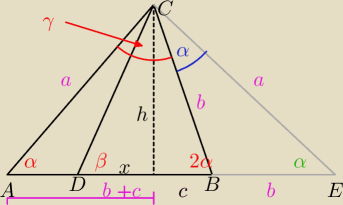
Można analogiczny rysunek:
γ = 180 − 3α (z sumy kątów w trójkącie ABC)
więc dorabiając kąt
α otrzymamy
γ + N[α]] = 180 − 2α ... stąd
α.
Stąd widzimy dwa trójkąty równoramienne (AEC oraz EBC). stąd
fioletowe długości (długość
'a' zbyteczna, ale już jest na rysunku

)
| | h | | h | |
sin(2α) = tgβ −−−> |
| = |
| −−−> x = b (rysunek absolutnie tego nie |
| | x | | b | |
reprezentuje)
Stąd |AD| = c ; |BD| = b+c ; |BC| = b
2 mar 19:26
Qba:
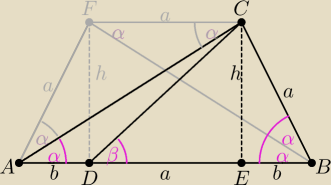
2 mar 19:39
matematycznyswir: Dziękuje za rozjaśnienie, faktycznie ma to sens!
3 mar 16:19
 W trójkącie ABC kąt ABC jest ostry i ma miarę dwa razy większą od miary α kąta BAC. Punkt D
jest punktem boku AB i β oznacza miarę kąta ostrego BDC.
Wykaż, że jeżeli sin2α = tgβ to BD = AD + BC
Utknąłem na tym, że BC=DE i dalej nie wiem jak to pociągnąć.
W trójkącie ABC kąt ABC jest ostry i ma miarę dwa razy większą od miary α kąta BAC. Punkt D
jest punktem boku AB i β oznacza miarę kąta ostrego BDC.
Wykaż, że jeżeli sin2α = tgβ to BD = AD + BC
Utknąłem na tym, że BC=DE i dalej nie wiem jak to pociągnąć.

 Można analogiczny rysunek:
γ = 180 − 3α (z sumy kątów w trójkącie ABC)
więc dorabiając kąt α otrzymamy γ + N[α]] = 180 − 2α ... stąd α.
Stąd widzimy dwa trójkąty równoramienne (AEC oraz EBC). stąd fioletowe długości (długość
'a' zbyteczna, ale już jest na rysunku
Można analogiczny rysunek:
γ = 180 − 3α (z sumy kątów w trójkącie ABC)
więc dorabiając kąt α otrzymamy γ + N[α]] = 180 − 2α ... stąd α.
Stąd widzimy dwa trójkąty równoramienne (AEC oraz EBC). stąd fioletowe długości (długość
'a' zbyteczna, ale już jest na rysunku  )
)
