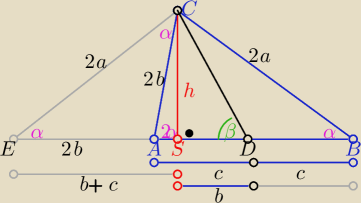
matura próbna 12grudnia 2024 Eta: https://arkusze.pl/maturalne/matematyka-2024-grudzien-probna-rozszerzona.pdf Podaję takie rozwiązanie : zad.12

	tgβ
Mamy obliczyć
	sin(2α)

po dorysowaniu ΔEAC ΔEAC∼ΔEBC z cechy (kkk) obydwa równoramienne

	2a		2b
to		=		⇒ (*)a2= b2+bc
	2b+2c		2a

	h		b+c		h
|ES|=|SB|=b +c i |SD|= b i sinα=		i cosα=		i tgβ=
	2a		2a		b

tgβ

1

1

1

1

h

2a

2a

W=

=

*tgβ*

*

=

*

*

*

2sinα*cosα

2

sinα

sinβ

2

b

h

b+c

	2a2		2a2
W=		i z (*) ⇒ W=
	b2+bc		a2

W= 2 ======

Eta: https://www.youtube.com/watch?v=47VwVwSoYRM

Bogdan:

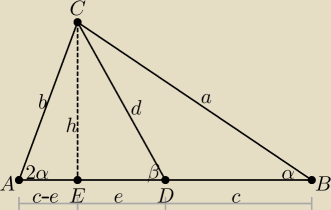
	a		b
albo tak: z twierdzenia sinusów w ΔABC:		=		⇒ b*2sinαcosα = asinα
	sin2α		sinα

stąd a = 2bcosα ΔEBC: c + e = a*cosα = 2bcos²α ΔAEC: c − e = b*cos2α = b(2cos²α − 1) −−−−−−−−−−−−−−−−−−−−−−−−−−−−− (−) 2e = b(2cos²α − 2cos²α + 1) = b ⇒ b = 2e

	tgα		b		2e
ΔAEC: h = b*sin2α i ΔEDC: h=e*tgβ ⇒ b*sin2α=e*tgβ ⇒		=		=		= 2
	sin2α		e		e

wredulus_inno_komputerowy: Etuś −−− trochę łatwiej byłoby po zauważeniu że |SD| = b po prostu zapisać:

	h
tgβ =
	b

	h
sin(2α) =
	2b

	tgβ
stąd od razu masz		= 2
	sin(2α)

Eta: Właśnie o tym też miałam napisać Oderwałam się od kompa ( piekłam pierniczki ) i już nie wróciłam

getin: Można też było dorysować dwusieczną kąta CAB która się przetnie bok BC w punkcie M, i wykorzystać podobieństwo ΔACM ~ ΔABC oraz Pitagorasy dla ΔASC i ΔSBC

getin: *która przetnie bok BC

SAIzou:

	h
tgβ =
	1   c 2

	h
sin2α =
	c

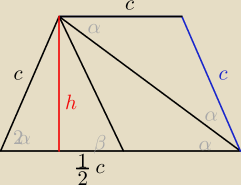
zatem ... szukany wynik to 2

S: Tak podaje CKE

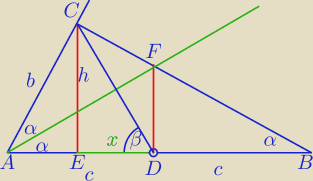
Mila: 1) h=bsin(2α) 2) AF − dwusieczna kąta A

CF		b
	=
FB		2c

3) CF||FD− Tales:

CF		x		b
	=		=
FB		c		2c

	b
x=
	2

4)

	h		2h
tgβ=		=
	b/2		b

tgβ=2 sin(2α)

tgβ
	=2
sin(2α)

==========

Kacper: Właśnie czekałem na ładne propozycje rozwiązań, bo te na CKE są koszmarne. Ładne tylko to z trapezem tam jest.

Qba:

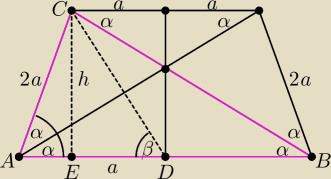
	h		h		tg(β)
Trapez:		=tg(β) i		=sin(2α) ⇒ a*tg(β)=2a*sin(2α) ⇒		=2
	a		2a		sin(2α)

Oba:

Kacper: Pytanie brzmi czy takie zadania nie są za trudne na maturze. Matura ma sprawdzać umiejętności z podstawy programowej, a nie wyłapywać dzieci do konkursów. Poza tym cześć rozwiązań oferowanych przez "ekspertów" CKE nie jest do zrobienia w czasie matury.