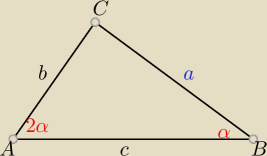
Trójkąt i kąty Mi Ka: W trójkącie ABC kąt przy wierzchołku A jest dwa razy większy niż kąt przy wierzchołku B . Boki AB i AC maja odpowiednio długośc c i b . Wyznaczyć długość trzeciego boku Mam do tego zadania wskazówkę Skorzystać z twierdzenia sinusów i cosinusów i BC=a=√b(b+c) więc rysunek zrobiłem ok Kąt przy wierzchołku C ma miare (180^o−3α) Jeśli skorzystam z twierdzenia sinusów to sin(180^o−3α)=sin(3α)

b		c
	=
sinα		sin(3α)

	b*sin(3α)
sinα=
	c

	b(3sinα−4sin3α)
sinα=
	c

	3bsinα−4bsin3α
sinα=
	c

sin(α)*c=3bsinα−4bsin³α 4sin³(α)b−3sin(α)b+sin(α)c=0 sinα[4sin²(α)b−3b+c]=0 sinα=0 odpada lub 4sin²(α)*b−3b+c=0 4sin²(α)*b=3b−c

	3b−c
sin2α=		musi byc >0 więc 3b>c i b>0 i c>0
	4b

Oblicze cos²α zeby skorzystac ze wzoru na cos(2α) do obliczenia a) cos²(α)=1−sin²α

	3b−c		4b		3b−c		4b−3b+c		b+c
cos2(α)=1−		=		−		=		=
	4b		4b		4b		4b		4b

cos(2α)=cos²α−sin²α

b+c

3b−c

b+c−3b+c

2c−2b

2(c−b)

c−b

cos(2α)=

−

=

=

=

=

4b

4b

4b

4b

4b

2b

Teraz obliczam długośc boku BC=a

	c−b
a2=b2+c2−2*b*c*
	2b

	2bc(c−b)
a2=b2+c2−
	2b

a²=b²+c²−c²+bc a²=b²+bc=b(b+c) a=√b(b+c) lub a=−√b(b+c) odpada czyli wyszło dobrze .

chichi: spójrz pod tym linkiem na moje rozwiązanie, @Eta i @Saizou https://matematykaszkolna.pl/forum/419814.html

Mi Ka: Ok. dziękuje

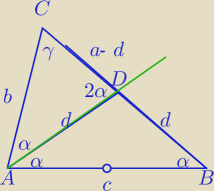Mila: II sposób 1) ΔADC∼ΔABC

b		a
	=
d		c

	bc
d=
	a

2) z tw. o dwusiecznej

b		c
	=
a−d		d

bd=ac−cd ⇔d(b+c)=ac 3) Z (1 i 2)

bc
	*(b+c)=ac ⇔b(b+c)=a2
a

a=√b*(b+c) =======

Mi Ka: Dobry wieczór Milu Pozdrawiam i dziękuje