Proszę o pomoc MACIEK: Dla jakich wartości współczynnika b podany przedział jest zbiorem wartości funkcji f(x) = −x² + bx + 1 ? a)(− ∞,1> b)(− ∞;,2> c)(−∞;5>

Jolanta: Wiesz co to jest wartość funkcji ?

ite: Trzeba skorzystać z informacji podanych na stronie: https://matematykaszkolna.pl/strona/1959.html 1/ Ramiona paraboli będącej wykresem podanej funkcji są skierowane do dołu, największą wartość funkcja osiągnie w wierzchołku.

	−Δ
2/ Wzór na drugą współrzędną wierzchołka to q=		.
	4a

3/ W przykładzie (a) największa wartość funkcji czyli druga współrzędna wierzchołka wynosi 1.

	−Δ
Stąd mamy równanie 1=		, z którego można wyliczyć b.
	4(−1)

MACIEK: to jest najwyzej polozony punkt na wykresie

aa: bez "nieśmiertelnej "delty

	−b
xw=p=
	2a

	b
xw=
	2

	b2		b2
yw=q= f(p)= −		+		+1
	4		2

	b2
q=		+1
	4

a) q=1

	b2
to		+1=1
	4

b=0 b) q=2 to ..... b=2 v b= −2 c) q=5 to ..... b= 4 v b= −4

Jolanta: Jeżeli a<0 jest to przedział od −∞ do wierzchołka Jeżeli a>0 Jet to przedział od wierzchołka do ∞

MACIEK : Czyli to będzie odpowiedz b?

Little Mint: Jak rozumiesz to zadnie? Co masz zrobić? Poza tym wartość funkcji o nie jest najwyższy punkt na wykresie Wartośc funkcji to jej wartośc dla konkretnego argumentu(czyli dla konkretnego x_sa Czym innym jest zbiór wartości funkcji . Co to jest to zajrzyj do podrecznika lub sprawdz na internecie .

Jolanta: Z odpowiedzi znasz współrzędna y wierzcholka y_w to q ite napisał ci jak to zrobic

Jolanta:

	−Δ
q=		w a). q=1. b) q=2 c) q=5
	4a

Δ= b²−4ac a=−1. c=1

	−Δ
a) q=
	4a

	−Δ
1=		/*(−4)
	−4

−4=−Δ Δ=4 Δ=b²−4ac 4=b²−4(−1)*1 4=b²+4 b²=0 b=0

Little Mint: Mój wpis 01 : 04 dotyczył tego co MACIEK napisał o godzinie 23 : 49 Dlatego zapytałem go czy rozumie treść zadania . Czy rozumie to ze dla kazdego podpunktu a) ,b) i c) ma wyznaczyć wartośc współczynnika b . a nie wybrac czy to jest a) lub b) lub c)

wredulus_pospolitus: Albo jeszcze inne podejście (tylko tutaj niestety w większym stopniu uczeń powinien wiedzieć 'co się dzieje') skoro funkcja wielomianowa W(x) = −x² + bx + 1 ma mieć ZW = (−∞ ; 'wartość' > to taką funkcję wielomianową można zapisać w postaci: W(x) = −(x+ 'coś')² + 'wartość' gdzie 'wartość' bierzemy z danego ZW. po przekształceniu dostaniemy: W(x) = −x² − 2*x*'coś' + 'wartość' − 'coś'² stąd: b = −2*'coś' natomiast: 1 = 'wartość' − 'coś'² jak już się bawimy to możemy wyznaczyć: b = −2*√ 'wartość' − 1 i wystarczy podstawić 'wartość' podaną ze ZW. Tylko tak jak pisałem na początku − uczeń musi mieć pojęcie 'co się dzieje' aby w ogóle dojść do tego punktu. Natomiast nagrodą będzie to, że po poświęceniu chwili czasu na wyprowadzenie tejże zależności, teraz każdy podpunkt robimy w 5 sekund: a) −> b = −2√1−1 = 0 b) −> b = −2√2−1 = −2*1 = −2 c) −> b = −2√5−1 = −2*2 = −4 i kończymy zadanie ... im więcej byłoby podpunktów, tym bardziej efektywne byłoby powyższe podejście (w porównaniu do 'standardowego podejścia').

wredulus_pospolitus: i oczywiście dałem dupy −−−> winno być b = ±2√'wartość' − 1

wredulus_pospolitus: Jeszcze inne podejście (ale to już trochę 'kombinowanie' ) 1. Zauważamy, że funkcja W(x) = −x² + bx + 1 bez względu na parametr 'b' będzie zawsze zawierać punkt (0;1). 2. Teraz musielibyśmy się odwołać do naszej wiedzy odnośnie zmiany wartości funkcji W(x) gdy 'oddalamy' się na osi liczbowej OX od wierzchołka paraboli. 3. Stosując wiedzę z (2) 'w drugą stronę' i wiedząc że punkt (0;1) zawsze należy do funkcji dojdziemy do równania: x_w² = 'wartość' − 1 (gdzie 'wartość' to wartość wzięta z ZW)

	b
co dalej odpowiada: xw = ±√'wartość' − 1 −−−> −		= ±√'wartość' − 1 −−−>
	2a

−−−> b = ±2√'wartość' − 1 (ponieważ a = −1)

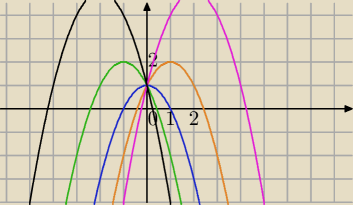
Mila: f(x)=−x²+bx+1 f(x)=a(x−p)²+q − postać kanoniczna a)

	b		b2
−x2+bx+1=−(x2−bx−1)=−[(x−		)2−		−1] ⇔
	2		4

	b		b2
f(x)= −(x−		)2+		+1
	2		4

	b2
q=		+1
	4

parabola skierowana w dół

b2
	+1=1
4

b=0 f(x)=−x²+1 b)

b2
	+1=2⇔b2=4⇔b=2 lub b=−2
4

f(x)=−x²−2x+1 lub f(x)=−x²+2x+1 c)

b2
	+1=5
4

b=4 lub=−4 f(x)=−x²+4x+1 lub f(x)=−x²−4x+1