Wykresy funkcji
Mi Ka:
Mamy dane dwie funkcje
y=f(x) i
y1=g(x)
Obie sa określone w tej samej dziedzinie D .
Trzeba sformułowac warunek konieczny i dostateczny na to aby :
a) wykresy tych funkcji były symetryczne względem prostej o równaniu y=k
b) wykresy tych funkcji były symetryczne względem prostej o równaniu x=p
W odpowiedzi jest tak
do a)
∀x∊D fx)−k=k−g(x)⇔∀x∊D f(x)+g(x)=2k
do b)
∀x∊D f(x)=g[p−(x−p)]⇔∀x∊D f(x)=g(2p−x)
tego zapisu nie rozumiem (co tu wstawić za g? )
Bardzo proszę o slowne wytlumaczenie obu podpunktow
Zadanie w zbiorze zadań jest oznaczone jako trudne
dziękuje
19 maj 22:16
Eta:
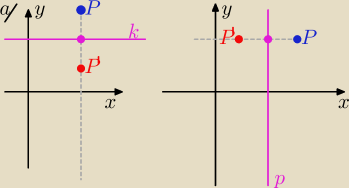
a) x
'=x
x
'=x
y
'= 2k−y ⇔ f(x)+g(x)=2k
y
'=y
x
'= 2p−x
y
'=y ⇔ f(x)=g(2p−x)
19 maj 23:22
Mi Ka:
Serdeczne dzięki
Eta
19 maj 23:59
20 maj 00:08
 a) x'=x
a) x'=x

 https://matematykaszkolna.pl/forum/330790.html
https://matematykaszkolna.pl/forum/330790.html