 Juz o to pytalem . Probuje to zrozumiec .
mamy dwie funkcje y=f(x) i y1= g(x) i one sa okreslone w tej samej dziedzinie
jaki jest warunek konieczny i dostateczny na to aby wykresy tych funkcji byly symetryczne
wzgldem prostej y=k
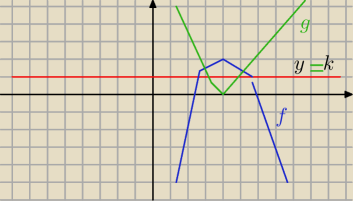
Zrobilem taki rysunek pogladowy (dla siebie
ale nie bardzo rozumiem odpowiedzi w zbiorze
Wykresy funkcji sa symetryczne wzgledem prostej o rownaniu y=k
⇔ dla kazdego x∊D f(x)−k=k−g(x)⇔ dla kazdego x∊D f(x)+g(x)=2k
Chcialem to sobie tlumaczyc np tak ze wspolrzedne xowe sa takie same ale yowe sie zmieniaja
ale to chyba mi nic nie da .
Juz o to pytalem . Probuje to zrozumiec .
mamy dwie funkcje y=f(x) i y1= g(x) i one sa okreslone w tej samej dziedzinie
jaki jest warunek konieczny i dostateczny na to aby wykresy tych funkcji byly symetryczne
wzgldem prostej y=k
Zrobilem taki rysunek pogladowy (dla siebie
ale nie bardzo rozumiem odpowiedzi w zbiorze
Wykresy funkcji sa symetryczne wzgledem prostej o rownaniu y=k
⇔ dla kazdego x∊D f(x)−k=k−g(x)⇔ dla kazdego x∊D f(x)+g(x)=2k
Chcialem to sobie tlumaczyc np tak ze wspolrzedne xowe sa takie same ale yowe sie zmieniaja
ale to chyba mi nic nie da .
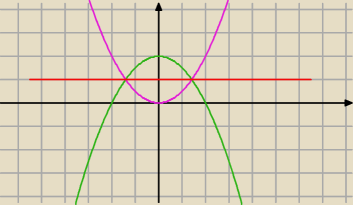
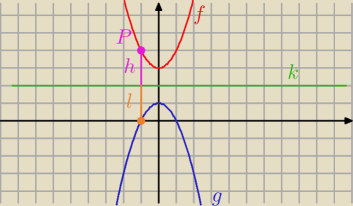 Chodzi o to że odległość h punktu P od prostej k to h=|f(P)−k|
analogicznie mamy odległość l=|g(P)−k|
żeby funkcje były symetryczne to l=k dla wszystkich P € D, stąd mamy
|f(P)−k|=|g(P)−k|
f(P)−k=g(P)−k albo f(P)−k=−g(P)+k
(1) f(P)=g(P) albo (2) f(P)+g(P)=2k
Przypadek (1) mówi o tym że dwie funkcje są równe, czyli g nie jest funkcją symetryczną do f.
Przypadek (2) jest tym o co nam właśnie chodzi
Chodzi o to że odległość h punktu P od prostej k to h=|f(P)−k|
analogicznie mamy odległość l=|g(P)−k|
żeby funkcje były symetryczne to l=k dla wszystkich P € D, stąd mamy
|f(P)−k|=|g(P)−k|
f(P)−k=g(P)−k albo f(P)−k=−g(P)+k
(1) f(P)=g(P) albo (2) f(P)+g(P)=2k
Przypadek (1) mówi o tym że dwie funkcje są równe, czyli g nie jest funkcją symetryczną do f.
Przypadek (2) jest tym o co nam właśnie chodzi 
| bf + bg | |
= k | |
| 2 |
 !: wzory funkcji kwadratowych oczywiście wyglądają tak:
f(x) = af(x−xof)2 + bf
g(x) = ag(x−xog)2 + bg
!: wzory funkcji kwadratowych oczywiście wyglądają tak:
f(x) = af(x−xof)2 + bf
g(x) = ag(x−xog)2 + bg

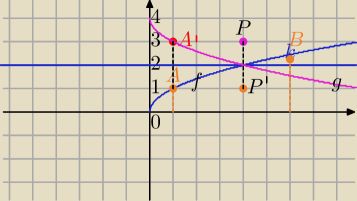 P=(x,y)∊wykresu funkcji f(x)
P'(x',y') symetryczny do P względem OX
Wzory opisujące przekształcenie płaszczyzny przez symetrię osiową względem osi
y=k
−−−−−−−−−−
x'=x
y'=2*k−y
==========
y+y'=2k
Przykład
k=2
f(x)=√x
A=(1,1)
A'=(1, 2*2−1)=(1,3)
wzór funkcji g(x) , której wykres powstał po przekształceniu wykresu f. f(x)
x=x'
y=2*2−y' ⇔y=4−y'
f(x)
y=√x
4−y'=√x
y'=−√x+4⇔
g(x)=−√x+4
P=(x,y)∊wykresu funkcji f(x)
P'(x',y') symetryczny do P względem OX
Wzory opisujące przekształcenie płaszczyzny przez symetrię osiową względem osi
y=k
−−−−−−−−−−
x'=x
y'=2*k−y
==========
y+y'=2k
Przykład
k=2
f(x)=√x
A=(1,1)
A'=(1, 2*2−1)=(1,3)
wzór funkcji g(x) , której wykres powstał po przekształceniu wykresu f. f(x)
x=x'
y=2*2−y' ⇔y=4−y'
f(x)
y=√x
4−y'=√x
y'=−√x+4⇔
g(x)=−√x+4
 Pozdrawiam
Wiesz ze pomyslalem przed chwila ze takze odpiszesz . dziekuje
Pozdrawiam
Wiesz ze pomyslalem przed chwila ze takze odpiszesz . dziekuje  Adamm mi kiedys odpisal podziekowalem mu bo myslaem ze zrozumialem ale okazalo sie ze nie
bardzo
Dlatego napisalem jeszce raz .
Adamm mi kiedys odpisal podziekowalem mu bo myslaem ze zrozumialem ale okazalo sie ze nie
bardzo
Dlatego napisalem jeszce raz .
 zasadę już napisałem
zasadę już napisałem 
 Ale to sprobuje juz jutro . dzisiaj slucham ladnych ballad
Ale to sprobuje juz jutro . dzisiaj slucham ladnych ballad 
 człowiek uczy się więcej jeśli sam czegoś doświadcza, w matematyce również.
człowiek uczy się więcej jeśli sam czegoś doświadcza, w matematyce również.
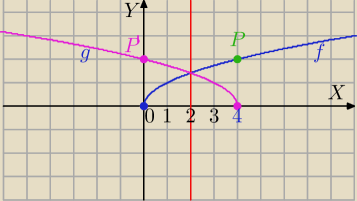 Wtedy masz :
x'=2k−x
y'=y
y=√x
k=2
P=(4,2)
P'=(2*2−4,2)=(0,2)
Wzór g(x):
x'=4−x
y'=y
−−−−−
Podstawiamy do wzoru f(x):
x=4−x' złożenie symetrii względem OY i translacji o wektor [2k,0]
y=y'
y'=√4−x'
g(x)=√4−x
Wnioski:
1)
Funkcją, której wykres jest symetryczny do funkcji y = f(x) względem prostej y = k
jest funkcja y = −f(x) + 2k
Złożenie symetrii względem OX i translacja (pionowo)
2) Funkcją, której wykres jest symetryczny do funkcji y = f(x) względem prostej x = k
jest funkcja y = f(−x + 2k)
Złożenie symetrii względem OY i translacji ( poziomo)
3) Wykresy są figurami przystającymi.
Wtedy masz :
x'=2k−x
y'=y
y=√x
k=2
P=(4,2)
P'=(2*2−4,2)=(0,2)
Wzór g(x):
x'=4−x
y'=y
−−−−−
Podstawiamy do wzoru f(x):
x=4−x' złożenie symetrii względem OY i translacji o wektor [2k,0]
y=y'
y'=√4−x'
g(x)=√4−x
Wnioski:
1)
Funkcją, której wykres jest symetryczny do funkcji y = f(x) względem prostej y = k
jest funkcja y = −f(x) + 2k
Złożenie symetrii względem OX i translacja (pionowo)
2) Funkcją, której wykres jest symetryczny do funkcji y = f(x) względem prostej x = k
jest funkcja y = f(−x + 2k)
Złożenie symetrii względem OY i translacji ( poziomo)
3) Wykresy są figurami przystającymi.

 I do zobaczenia na forum po poludniu
I do zobaczenia na forum po poludniu 

 Bede czekal w takim razie . Bardzo dziekuje
Bede czekal w takim razie . Bardzo dziekuje 

 Raczej nie . Mieszkam na wiosce wiec raczej w poniedzialek ,wtorek .
Naprawde dziekuje . Dam znac jak dojdzie
Raczej nie . Mieszkam na wiosce wiec raczej w poniedzialek ,wtorek .
Naprawde dziekuje . Dam znac jak dojdzie 



 To az tak sie nie pali . Od tego nie zalezy moje byc albo nie byc
To az tak sie nie pali . Od tego nie zalezy moje byc albo nie byc  Ale w sumie masz racje . Skoro daja taka opcje to tak jak mowisz . Powinni ja realizowac .
Ale w sumie masz racje . Skoro daja taka opcje to tak jak mowisz . Powinni ja realizowac .
 Jak przygotowania do wyjazdu do Wroclawia ?
Jak przygotowania do wyjazdu do Wroclawia ?
 więc sprzeczanie się będzie przy kawie i ciastku..
więc sprzeczanie się będzie przy kawie i ciastku.. a
ona to może kiedyś wykorzysta w sprzeczkach o normy
a
ona to może kiedyś wykorzysta w sprzeczkach o normy 

 Kiedys chyba zespol Alibabki spiewal taka ladna piosenke Jak dobrze miec sasiada
Kiedys chyba zespol Alibabki spiewal taka ladna piosenke Jak dobrze miec sasiada  I teraz okazuje sie ze takze dobrze jest miec sasiadke
I teraz okazuje sie ze takze dobrze jest miec sasiadke 



 ( przynajmniej teraz)
( przynajmniej teraz) 
 Jak to mowia [Nie boj zaby zaba w wodzie nie bodzie ]]
Jak to mowia [Nie boj zaby zaba w wodzie nie bodzie ]]  Nie jest to przyjemne sam musze isc zalozyc plombe .
Nie jest to przyjemne sam musze isc zalozyc plombe .