planimetria matura rozszerzona Patrycja: 1. Oblicz długość środkowej CD w trójkącie ABC o bokach długości a=10cm, b=12cm, c=20cm. 2. W trójkącie ABC mamy dane |AC|=8, |BC|=12 oraz |∡ACB| = 120st. . Przez wierzchołek C poprowadzono prostą prostopadłą do boku BC. Przecięła ona bok AB w punkcie D. Oblicz długość odcinka CD.

chichi:

	1
|CD| =		√2*102 + 2*122 − 202 = √22
	2

Patrycja: dlaczego tak?

chichi: bo taki jest wzór na środkową, który można w prosty sposób wyprowadzić https://www.naukowiec.org/wiedza/matematyka/srodkowa-trojkata_584.html

chichi: tam jest z literówką... tu masz bez literówki https://www.megamatma.pl/uczniowie/wzory/geometria-analityczna/srodowe-bokow-trojkata

Patrycja: hmmm, a to wchodzi w zakres liceum? bo kurczę jakoś go nie pamiętam widzę ze to jest jakos wyprowadzone z cosinusow ale jakos koslawie, bo tam nie ma przecież kąta:?

Patrycja: :(

chichi: https://matematykaszkolna.pl/forum/419269.html tutaj napisałem szkic dowodu, wystarczy wstawić i uprościć. jeżeli nie chcesz korzystać z gotowego wzoru, to przeprowadź tę procedurę na liczbach, które masz

Patrycja: super! już rozumiem! inteligentne i szczwane to rozwiązanie, dziękuje a drugie masz moze jakas podpowiedz?

Patrycja: okej mam juz jeszcze raz dziekuje za pomoc

chichi:

	1		1
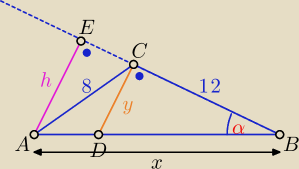
PABC =		* 8 * 12 * sin(120o) = 24√3, no ale też PABC =		* 12 * h = 6h,
	2		2

zatem mamy, że h = 4√3. z tw. Carnota (tw. cosinusów) w ΔABC otrzymasz, że x = 4√19.

	y		12
z tw. Pit. w ΔABE mamy, że |EB| = 16. ΔABE ∼ ΔDBC, stąd		=		⇔ y = 3√3
	4√3		16

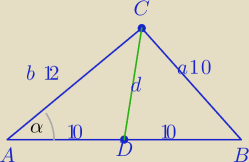Mila: Z zast,tw. cosinusów. jeśli nie znasz wzorów na dł. środkowych. 1) ΔABC: 10²=20²+12²−2*20*12 cosα

	37
cosα=
	40

2) W ΔADC:

	37
d2=102+122−2*10*12*
	40

d²=22 d=√22 2)

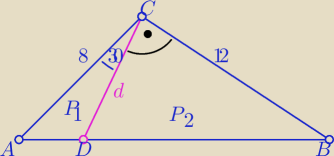aa: zad2/

	1
PABC=		*8*12*sin120o= 24√3
	2

	1		1
P1=		*8*d*sin30o =2d i P2=		*d*12=6d
	2		2

P₁+P₂=P 8d=24√3 d= 3√3