Oblicz pole Paluszek: W trójkącie dane są długości 2 boków: 3 cm i 5 cm i długość środkowej poprowadzonej do 3 boku równa 2cm. oblicz pole trójkąta i pole koła opisanego na trójkącie.

chichi: niech d (=2), będzie długością środkowej opuszczonej na trzeci bok długości x (x>0), wówczas:

	√32 + 52 − x2
2 =		⇔ x = ...
	2

	abc		L
P =		i jeszcze może np. wzór Herona? P = √p(p−a)(p−b)(p−c), gdzie p =
	4R		2

chichi: chochlik:

	√2*32 + 2*52 − x2
2 =		, zapomniałem o 2 z pośpiechu
	2

Paluszek: Dzięki wielkie

Paluszek: A dałoby się tu zastosować twierdzenie cosinusów?

chichi: jasne, w tym wzorze na środkową w wyprowadzeniu używa się dwukrotnie twierdzenia cosinusów

chichi:

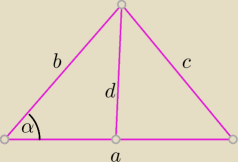
	1		1
(1) d2 = b2 + (		a)2 − 2 *		a * b * cos(α)
	2		2

	c2 − a2 − b2
(2) c2 = a2 + b2 − 2ab * cos(α) ⇒ cos(α) =
	−2ab

wstawić teraz do (1), uprościć i spierwiastkować i mamy wzór