SurjekcjA Ola: Czy może ktoś na chłopski rozum wytłumaczyć iniekcje surjekcje bijekcje

wredulus_pospolitus: iniekcja −−− inaczej −−− funkcja różnowartościowa. Na chłopski rozum −−− gdy funkcja (w swojej dziedzinie) nie przyjmuje żadnej wartości 'y' więcej niż raz. Np. f(x) = x² gdzie D_f = R nie jest równowartościowa, bo 1 = 1² ale także 1 = (−1)² (dwa różne 'x' a ta sama wartość funkcji) f(x) = x² gdzie D_f = R₊ już jest różnowartościowa

wredulus_pospolitus: suriekcja −−− inaczej −−− funkcja 'na' Na chłopski rozum −−− gdy każda wartość z przeciwdziedziny jest przynajmniej raz przyjmowana. Alternatywne wyjaśnienie: gdy przeciwdziedzina jest równa zbiorowi wartości funkcji (dla zadanej dziedziny). Np. f: R −> R f(x) = x² nie jest funkcją 'na' ponieważ funkcja f(x) nigdy nie przyjmie wartości (np.) −5 f: R −> [−1 ; +∞) f(x) = x² nie jest funkcją 'na' ponieważ funkcja f(x) nigdy nie przyjmie wartości (np.) −1 f: R −> [0 ; +∞) f(x) = x² jest funkcją 'na'

6latek: I komu to przeszkadzało ze kiedys było odwzorowanie na odwzorowanie w

wredulus_pospolitus: bijekcja Na chłopski rozum −−− gdy jest zarówno suriekcją jak i iniekcją. Wtedy też funkcja f(x) będzie funkcją odwracalną. Można dodatkowo zauważyć, że: 1. Jeżeli chcielibyśmy 'odwrócić' funkcję która nie jest różnowartościowa (np. f: R −> [0 ; +∞) f(x) = x²) to dla tego samego x (w tym przypadku np. x = 1) mielibyśmy dwie różne wartości funkcji (y) −−−− czyli to nie byłaby funkcja 2. Jeżeli chcielibyśmy 'odwrócić' funkcję która nie jest 'na' (np. f: [0;+∞) −> R f(x) = x²) to otrzymamy funkcję której dziedzina (w tym przypadku D_f⁻¹ = R) dla której istnieją takie x'sy dla których funkcja nie przyjmuje ŻADNEJ wartości (np. f⁻¹(−5) nie istnieje) związku z tym −−− to nie jest funkcja.

6latek: Tłumaczenie na chłopski rozum jest dla mnie najlepsze Więc idzie na pulpit

Ola: a czym jest przeciwdziedzina? To nie jest zbior wartosci funkcji?

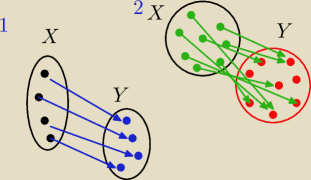
6latek: czasami zbiór wartosci funkcji nie jest równy przeciwdziedzinie funkcji W odwzorowaniu nr 2 w zbiorze Y zostaja niewykorzystane dwa elementy

Ola: czyli przeciwdziedzina to?

6latek: Dobrze Olu . A co masz napisane na ten temat w podręczniku ?

Ola: w tym rzecz ze narazie na studiach brak podrecznika i same wyklady w ktorych nie do konca jest ta algebra i analiza dobrze wytlumaczona

6latek: Zobacz tutaj co na temat przeciwdziedziny i zbioru wartości pisze Bogdan https://matematykaszkolna.pl/forum/108610.html

wredulus_pospolitus: Przeciwdziena to zbiór do którego należą wszystkie 'y' (wszystkie przyjmowane przez funkcję wartości), podczas gdy zbiór wartości funkcji to najmniejszy taki zbiór do którego należą wszystkie 'y'.

Adamm: @Ola Funkcja w liceum to po prostu coś co bierze wartości z dziedziny i coś oddaje. To nie wystarcza dla wyższej matematyki. Tutaj jest inaczej. Funcja f:X → Y składa się z dziedziny X, dla każdego x ∊ X, pewnego punktu f(x)∊ Y. Ten zbiór Y jest nazywany przeciwdziedziną. Nie musi to być zbiór wartości, ale zawsze musi być podany.

Ola: jakos nie widze roznicy

Ola: no ale jaka jest roznica miedzy przeciwdziedzina a zwf? Te y ktore sa przypisane do x w funkcji to zwf wiec czym jest niby przeciwdziedzina

Adamm: Funkcje na studiach składają się ze zbioru X, Y i wykresu graph(f) ⊆ X x Y który jest zbiorem par (x, y). Dla każdego x ∊ X istnieje dokładnie jeden y ∊ Y dla którego (x, y) ∊ graph(f). Oznaczamy wtedy y = f(x).

Adamm: Jeśli masz f₁:X → Y₁ oraz f₂:X → Y₂, to nawet jeśli f₁(x) = f₂(x) dla każdego x ∊ X, formalnie nie są to te same funkcje, chyba że Y₁ = Y₂.

wredulus_pospolitus: tak jak napisałem −−−− przeciwdziedzina musi zawierać wszystkie wartości przyjmowane przez funkcję (ale może zawierać także takiej, jakich funkcja nie przyjmuje) Zbiór wartości to taki zbiór który posiada wszystkie wartości przyjmowane przez funkcję i ani jednego więcej (ani jednego który przez tą funkcję nie jest przyjmowany)

Adamm: Zbiór wartości to zbiór {f(x) : x ∊ X} i może on się różnić od Y. Może istnieć y ∊ Y taki że nie istnieje x ∊ X że y = f(x). Np. funcja f: R → R dana przez f(x) = x². Nie istnieje x dla którego x² = −1. Przeciwdziedzina to R, ale zbiór wartości to [0, ∞).

Ola: czyli zwf to to co przyjmuje funkcja a przeciwdziedzina to wszystko na osi y?

wredulus_pospolitus: nie koniecznie wszystko ... ale minimum tyle o zbiór wartości. przykładowo dla funkcji f(x) = x² ZW = [0 ; +∞) prawda Prawda. Przeciwdziedzina może być dowolnym zbiorem który zawiera ZW = [0; +∞) więc na przykład R albo (−5 , +∞) nawet {−1} u [0 , +∞) i z punktu widzenia matematyki funkcje: f:R −> R , f(x) = x² oraz g: R −> (−5, + ∞), g(x) = x² oraz h: R −> [0, + ∞), h(x) = x² to są trzy RÓŻNE funkcje (ponieważ posiadają inną przeciwdziedzinę). Przy czym tylko funkcja h(x) jest funkcją 'na' ponieważ jej przeciwdziedzina jest równa zbiorowi wartości tejże funkcji.

Adamm: Ważne jest dla nas czym jest f(x), ale nie czym jest obraz/zbiór wartości funkcji f

Adamm: Powiedzmy f(x) to jest wektor. Ale po co ci wiedzieć co to za zbiór wektorów jest f[X]?

wredulus_pospolitus: Adamm ... z całym szacunkiem, ale nie potrzebnie wprowadzasz pojęcia, których Ola raczej nie zrozumie.

Ola: czyli przeciwdziedzina to zbior wartosci funkcji + jakies inne zbiory tak?

wredulus_pospolitus: tak ... o ile 'jakieś inne zbiory' to także może być zbiór pusty (innymi słowy przeciwdziedziną może być dokładnie zbiór wartości funkcji )

Adamm: Przeciwdziedzina to jest w ogóle bardziej fundamentalne pojęcie niż zbiór wartości W ogóle to zapomnij co to jest zbiór wartości bo to nie ma ze sobą nic wspólnego

Ola: a od czego zalezy czemu mozze istniec jakis inny zbior niz ten zbior wartosci funkcji

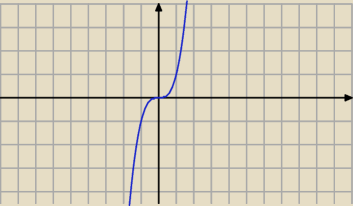
6latek: Weżmy np y=x³ ZW=Y=(−∞,∞) redukuje ją do przedziału <−3,3> więc mam ZW=<−27,27> Teraz sobie wezmę funkcje y=sin(x) ZW=Y=<−1,1> redukuje ją do przedziału <−π,2π> ZW=Y=<−1,1> a powinien ulec zmianie bo funkcja została zredukowana tak jak porzednia