proszę o rozwiązanie anna: wyznacz wartości parametru m ∊ R dla których równanie m16^x+ (2m − 1 )*4^x + m + 2 =0 ma co najmniej jedno rozwiązanie podstawiłam za 4^x = t t > 0 mt² + (2m − 1 )*t + m + 2 =0 ponawiam prośbę o rozwiązanie zadania

6latek: Napisz odpowiedz do zadania jeśli jest

Monika: Początek masz dobrze. Przypadek 1. Traktujesz to równanie jako kwadratowe i zrób założenie, że współczynnik a jest różny od zera, czyli m różne od zera. Wylicz teraz deltę podstawiając za a=m, b=2m−1, c=m+2. Aby równanie miało co najmniej 1 rozwiązanie, delta musi być większa lub równa 0. Mnie delta wyszła −12m+1, z czego masz m mniejsze lub równe 1/12. Przypadek 2. Rozpatrujesz przypadek dla m=0, czyli warunek, że funkcja nie jest kwadratowa tylko liniowa. Kiedy podstawisz do równania wszędzie m=0, otrzymasz −t +2 =0, więc t=2. Wtedy t=2 przyrównasz do pomocniczego podstawienia i masz 4^x=t 4^x=2 2^2x=2¹ 2x = 1 x=1/2 Odp. Dla m=0 jest jedno rozwiązanie x=1/2

6latek: Moniko zobacz wpis ite https://matematykaszkolna.pl/forum/417905.html Wtedy jaki iloczyn,jaka suma tych rozwiązań .

Monika: 6−latek Obejrzałam to rozw. z linku, ale troszkę nie rozumiem, po co trzeba robić założenie do wzorów Viete'a

anna: mam pytanie czy trzeba zastosować wzory Viete^,a i jaka ma być suma i iloczyn

anna: nie mam odpowiedzi do zadania

ite: Rozwiązanie równania ze zmienną pomocniczą z 16 paź 23:40 za pomocą samego wyróżnika / Δ≥0 / prowadzi do wybrania wszystkich fioletowych rozwiązań. https://www.geogebra.org/graphing/enjvpnbp Dodanie warunków, które zaczęłam podawać o 9 paź 22:13 w wątku https://matematykaszkolna.pl/forum/417905.html pozwala wybrać poprawne rozwiązania dodatnie, i odrzucić wyniki nieprawidłowe − mimo dodatniego wyróżnika. A wybrać je można, korzystając ze wzorów Viete'a. Dlatego warunki z tymi wzorami są niezbędne. https://www.geogebra.org/graphing/kuetaakb

ite: @anna, @Monika czy te animacje w geogebrze wyjaśniły cokolwiek?

Adamm: Eta w linku od geogebry? Podejrzane

Adamm: f(x) = mx²+(2m−1)x+m+2 m = 0 wiadomo Δ ≥ 0 to można po prostu zobaczyć znak f(0) = m+2

Adamm: Jeszcze znak −(2m−1)/2m

Adamm: I oczywiście m

anna: czy taki warunek jest poprawny t₁*t₂ > 0 i t₁ + t₂ >0 t₁*t₂ > 0 ⇒(m + 2)m >0 ⇒ m ∊ (−∞;0)∪ ( −2 ; +∞) t₁ + t₂ >0 ⇒ −(2m − 1 ) /m > 0 ⇒ m ∊ (−∞;0)∪ ( ¹₂; +∞)

ite: 15:44 to szukanie dwóch miejsc zerowych dodatnich (m + 2)m>0 ⇒ m∊(−∞;−2) ∪ (0 ; +∞)

−(2m − 1)		1
	>0 ⇒ m∊(0;		)
m		2

	1
wcześniej były warunki m≠0 i Δ>0 czyli m∊(0;		)
	12

	1
czyli w sumie m∊(0;		)
	12

Ale to jest tylko część rozwiązania, we wcześniejszym wątku miałaby u mnie numer 3C. Jest jeszcze rozwiązanie znalezione przez Monikę 23:40 dla m=0 oraz sprawdzenie przypadków 2B i 3B, które jak widać z animacji dają rozwiązania.

ite: @Milu możesz wyjaśnić rozwiązanie tego zadania? Ja nie umiem przekazać, czym skutkuje ten warunek co najmniej jedno rozwiązanie.

Monika: Oznacza jedno lub więcej rozwiązań.

Monika: W nocy myślałam nad tym, czemu należy sięgnąć w tym zadaniu do wzorów Viete'a, ale już zajarzyłam. Niesamowite jest to zadanie.

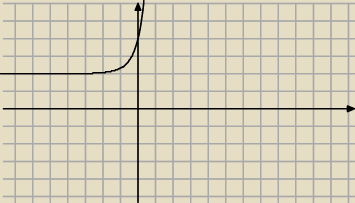
6latek: Wykres funkcji y=16^x+4^x+2 jest taki tak sie zastanawiam czu funkcja y=m*16^x+(2m−1)*4^x+m+2 może przecinac os OX w dwoch miejscach skoro jest co najmniej ?

ite: @6latku Wprowadziliśmy zmienną pomocniczą t=4^x. Znajdujemy rozwiązania równania ze zmienną pomocniczą. Ponieważ t=4^x>0, wybieramy z nich tylko te, gdy t>0 (czyli dodatnie). Skoro funkcja g(x)=4^x jest różnowartościowa, każde znalezione dodatnie rozwiązanie t "doprowadzi" nas do jednego rozwiązania równania t=4^x. Teraz pytanie, czy funkcja f(x)=m16^x+ (2m−1)*4^x+m+2 może przecinać oś OX w dwóch miejscach. Jeśli istnieje taka wartość parametru m, dla której równanie ze zmienną pomocniczą ma dwa rozwiązania dodatnie, to równanie wyjściowe również będzie mieć dwa rozwiązania. Jak wynika z obliczeń z 17 paź 16:54 dwa rozwiązania istnieją gdy parametr m przyjmuje wartości

	1
z przedziału m∊(0;		).
	12

Na animacji https://www.geogebra.org/graphing/ytz964tq przedstawiającej funkcję f(x)=m16^x+ (2m−1)*4^x+m+2, można zobaczyć, że dla

	1
m∊(0;		) są dwa rozwiązania.
	12

ite: @Monika czyli zadanie nie okazało się usypiające : )

6latek: Dobry wieczór ite Robiłem tutaj wykres dla kilku wartosci m i dla pewneo m wyszedł mi taki załamany wykres ale już kilka razy tutaj wykres wyszdł nie tak wiec pomyślalem ze to pomyłka .

ite: @6latku pewnie nie zwróciłeś uwagi na to, że o 17:51 dodałeś trzy wyrażenia dodatnie, więc ich suma 16^x+4^x+2 i nie może mieć wartości zero.

ite: Tym, którzy nie chcą korzystać ze wzorów Viete'a, Adamm we wpisach 15:10−15:19 podpowiedział inny sposób ustalenia, jaki znak mają rozwiązania równania ze zmienną pomocniczą !

chichi: nie tylko w rachunku prawdopodobienstwa dużym ułatwieniem często jest zbadanie zdarzenia przeciwnego, przenosząc to na to zadanie − dużo łatwiej jest odpowiedzieć na pytanie przeciwne, mianowicie kiedy oba rozwiązania będą nie dodatnie? omijamy w ten sposób wszystkie te przypadki z osobna, o których pisała @ite, zatem:

⎧	t1 + t2 ≤ 0
⎨
⎩	t1t2 ≥ 0

następnie wziąć dopełnienie zbioru będącego rozw. tego układu i złapać w przekrój z warunkiem z Δ i po krzyku, to wg mnie najprostsza droga

ite: Najprostsza i mam nadzieję, że przekonywująca dla autorki pytania. Mój sposób tłumaczenia ani rozbijanie na przypadki nie były skuteczne (w końcu autorka wstawiła to zadania po raz drugi). Krzyku nie było, ale pisania wyszło sporo.

anna: dziękuję bardzo wszystkim