wzór ogólny frycek: mam wyrazy początkowe: a₁ = 1 a₂ = 2 a₃ = 5 a₄ = 14 a₅ = 40 szukam wzoru ogólnego. Na razie wiem tylko tyle: a_n = a_n−1 + a_n−2. Próbowałem już z wieloma liczbami ale jak dla jednego zadziała to dla drugiego się pierdoli.Mam np. wyraz a3=5. Napisałem: a₃ = a₃₋₁+a₃₋₂ a₃ = a₂+a₁ a₃ = 2 + 1 = 3 czyli nie może być bo musze mieć 5 czyli pozostaje tylko 2 no to wzór ogólny to by było a_n = a_n−1+a_n−2+2? No to zobaczmy dalej? a₄ = a₃ + a₂ +2 a₄ = 5 + 2 + 2 = 9 czyli już nie działa, a mnie szlag trafia. Jak to dziadostwo ogarnąć? Ma ktoś pomysł?

wredulus_pospolitus: To co podałeś TO NIE JEST WZÓR OGÓLNY. Jaka jest DOKŁADNIE treść zadania

frycek: Widziałem podobne zadanie już na tym forum to jest lekko zmodyfikowane: https://zapodaj.net/plik-j0X7FF8d4Q treść jest ta sama tylko rysunek nieco się różni

wredulus_pospolitus: A widziałeś jaki ja tam wzór zaproponowałem Oraz wyjaśnienie w jaki sposób do niego doszedłem Mało tego −−− rysunek (w porównaniu z samymi suchymi liczbami) po pierwsze ułatwia wpadnięcie na rozwiązanie, po drugie eliminuje wiele innych przypadków które mogłyby być rozpatrywane. Tak więc −−− proszę o oryginalną treść zadania, a nie Twoją interpretację

wredulus_pospolitus: AAA ... to jest oryginalna treść Okey No i zajęło mi to (po zauważeniu że to ogrodzenie różni się od tego co wtedy było podane), całe 30 sekund aby wpaść na pomysł jaki to może być wzór

frycek: Ja to trochę inaczej chciałem zrobić. Te poszczególne etapy potraktować jako wyrazy początkowe. Zapisać sobie to tak: n a_n 1 1 2 2 3 5 4 14 5 40 Dlaczego tak? Policzyłem ilość prętów w każdym etapie budowy. W pierwszym jest 1 pręt, w drugim 2, w trzecim 5, w czwartym 14, a w piątym 40 i na tej podstawie znaleźć wzór ogólny. Czyli np. jak obliczyć a5, które w tym przypadku równa się 40 za pomocą a4, które równa się 14 i a3, które równa się 5. I tak z każdym wyrazem.

frycek: Ja ci przedstawiłem swoją interpretacje na rozwiązanie tego zadania, którą podałem wyżej.

wredulus_pospolitus: chodzi oto ... że na suchych liczbach nie masz wszystkich informacji, które przekazują Ci rysunki ... z tego powodu: 1. utrudniasz sobie zadanie 2. zwiększasz szansę na to, że dojdziesz do jakiegoś wyniku który dla liczb może i będzie miał sens, ale dla rysunku z pewnością sensu nie będzie miał

frycek: Bo tamto, które widziałem też można rozwiązać w taki sposób, który podałem. I uzyskałem wzór taki jaki tobie wyszedł robiąc to w taki sposób jak wyżej. Tylko dlaczego tutaj nie działa?

wredulus_pospolitus: Ważna jest zarówno ilość prętów 'grubych' i 'cienkich' jak i ich ułożenie ... ile prętów 'cienkich' jest pomiędzy 'grubymi'. Jeszcze raz odsyłam do tamtego zadania z prętami i mojej wypowiedzi w jaki sposób wpadłem na rozwiązanie. Spróbuj to zastosować tutaj.

frycek: Dobra spróbuje. W razie czego będę pisał. Na razie dzięki za pomoc.

wredulus_pospolitus: dobra ... zajęło mi to trochę dłużej niż te 30 sekund (początkowo źle spojrzałem na rysunek). Mam jakieś tam rozwiązanie, które pasuje ... ale czy na pewno pasuje ... któż to wie, bo 'stworzenie płotu' nie jest tak intuicyjne i jednoznaczne jak w poprzednim tego typu zadaniu.

frycek: No właśnie i gdzie tu jest pies pogrzebany?

wredulus_pospolitus: i taka jedna mała uwaga −−− trudno, żeby Ci coś wyszło z przedstawienia liczbowego skoro a₅ = 41 a nie 40 I jak tam ... coś Ci się udało wykombinować

frycek: nie jeszcze kombinuje. Analizowałem to co rozpisałeś w poprzednim zadaniu, i nawet idzie się w tym połapać ale tutaj już nie jest to takie proste.

frycek: Nie wiem czy dobrze kombinuje jakby co to wal. Staram się kombinaować w podobny sposób jak ty przy poprzednim zadaniu. Mianowicie. W x3 czyli w trzecim etapie budowy mamy 4 cienkie pręty lecz w x2 są tylko 2 więc ich liczba się podwoiła więc biore 2 razy x2 i dorzucam x1 tylko z kolei w 4 etapie czyli w x4 liczba tych grubych mi się podwaja.

frycek: więc na początku bym napisał: a_n = 2_an−1 ... tu za chwile koljena część

frycek: dlaczego 2_an−1? No bo w x3 mam 4 te cienki ale w x2 mam 2 więc wystarczy jak dorzuce te 2 i mam 4. Jak miałbym w całości to napisać to bym wziął tak: an = 2_an−1 + a_n−2(bo na początku w x3 mam tylko jednego grubasa) i + 1 bo w x3 mam jednego grubasa ale w x4 są dwa więc dorzucam jeszcze jeden. Nie wiem czy to dobry wzór: a_n = 2_a{n−1} + a_n−2 + 1

wredulus_pospolitus: pytanie − wskazówka : zwróć uwagę na liczbę 'grubasów' w a₅ i jak to się ma z ilościami 'grubasów' w a₃ i a₄

frycek: jest 7 grubasów w a5 w a4 2, a w a3 1.

frycek: w a5 tych cienkich prętów między grubasami jest (6,4,6,6,4,6)

frycek: bo staram sie coś podobnego wykombinować do tego co napisałeś tu: https://matematykaszkolna.pl/forum/417764.html widze, że x3 składa sie z 4 'cieniasów' i jednego 'grubasa'. W x2 są tylko 2 grubasy więc do x3 też musze dołożyć 2 żeby było 4 no i dorzucam 1 cieniasa

Rrg: Jak to jak ma się ilość grubasów z a5 do grubasów z a4 i a3? W a3 jest jeden w a4 też dochodzi jeszcze jeden grubas a w a5 liczba cieniasów jest różna pomiędzy grubasami. W każdym etapie od x3 do x5 zmienia się liczba cieniasów w zależności od ilości grubasów bo inaczej już tego nie rozumiem.

frycek : Tak mnie dobija to zadanie, że aż Nick mi się zmienił.

. : Wskazowka do wskazówki − − − ile musiałbyś wziąć a₃ a ile a₄ aby zgodziła się ilość 'grubasow' w a₅ Jakie są możliwości Zacznij od tego

frycek : Jeśli grubasów w a5 jest 7, a w a3 jest 1 no to możliwe kombinacje wg mnie to 1+6 1+5+1 1+2+4 A w a4 są 2 grubasy no to może być 2+4+1 2+3+2 2+2+3 Nie bardzo wiem czy to o to chodzi? A można brać te grubasy jednocześnie z a3 i a4 bo mi przyszło tak do głowy ale nie wiem. Tylko taka sugestia.

. : Chodzi oto że masz takie możliwości 7a₃ + 0a₄ 5a₃ + 1a₄ 3a₃ + 2a₄ 1a₃ + 3a₄ Ttlko takie kombinacje dadzą odpowiednią (równa 7) ilość 'grubasów' To już zawezilo do 4 możliwości 'rdzen' wzoru którego szukasz

frycek : W porządku. A w takim razie można już przechodzić do pisania wzoru czy czegoś jeszcze brakuje?

. : Człowieku − czemu mi zadajesz pytanie skoro sam możesz sobie odpowiedzieć na to pytanie? Masz czterech 'podejrzanych' sprawdź co się biedzie działo z 'cienkimi pretami' w każdym przypadku i co się będzie działo z pretami ogólnie także dla innych etapów (czyli stworzenie a₃ i a₄)

. : Jeszcze jedna sprawa − obserwując tylko i wyłącznie jak wyglądaja a₃, a₄ a jak wygląda a₅ można domyślić się czy będziemy musieli doda, odjąć czy nic nie robić w sprawie pojedynczych prętów oraz podejrzewasz o jakiej ilości mówimy.

frycek: @. : a jakbyś zrobił przykład jak to zrobić. Może łatwiej będzie.

wredulus_pospolitus: analogicznie do tego co wtedy robiłem niestety 'spostrzegawczości i umiejętności kombinowania' Ciebie nie nauczę

frycek : Na przykład ten pierwszy przykład z brzegu co napisałeś 7a₃+0a₄=7×1 bo mam jednego grubasa w a₃ + 0×2 bo są dwa grubasy w a₄ co daje nam 7 grubasów w a₅. I co dalej?

frycek : Wredulusie: to na pewno się zgadza lecz problem polega na tym że ty czy @. : rozwiązaliście pewnie setki takich zadań. A ja nie rozwiązuje tego na codzień. Raczej sporadycznie. Dlatego to co do mnie tu piszecie wydaje mi się czarną magią. Ale myślę że nie powinienem mieć problemu że zrozumieniem. W końcu nie bez powodu znalazłem to forum

wredulus_pospolitus: "." to także 'mła' tyle że z komórki Więc jeszcze raz: 1. Obserwujemy ile 'grubasów' mamy w a₅ 2. Na postawie tego, typujemy 4 przypadki z kombinacji x*a₃ + y*a₄ tak aby ilość 'grubasów' się zgadzała 3. Teraz patrzymy jak będą wyglądały 'cienkie' szczebla (ich ilość) pomiędzy 'grubasami' gdy każdego z danego przypadku 4. Odrzucamy te przypadki z których nie możemy uzyskać odpowiedniej sekwencji 'cieniasów' pomiędzy 'grubasami' To Ty musisz kombinować, to że ja Ci dam gotowe rozwiązanie w niczym Ci nie pomoże − analogicznego zadania nie będziesz w stanie zrobić. Zanim tego sobie w główce nie ułożysz, to nawet jak Ci wyjaśnię w jaki sposób wykombinowałem rozwiązanie, może Ci to nic nie dać, bo po prostu nie będziesz 'ustawiony na kombinowanie' i nie zrozumiesz mojego toku myślenia −−−− co pokazuje to co dotychczas mieliśmy.

wredulus_pospolitus: I nie − nie robiłem takich zadań w setkach. Można by rzec, że jest to jedno z nielicznych zadań tego typu które robiłem. To niestety jest zadanie bardziej na mentalność (umiejętność kombinowania, próbowania, wyciągania wniosków z prób) niż na umiejętność liczenia.

frycek : Jedyne co dostrzegam patrząc na te rysunki to to, że pomiędzy grubasami są 4 cienkie pręty. Są 2 pręty po obu stronach, a pomiędzy nimi 4 cieniasy potem jest 6 cieniasów i znowu grubas , 4 cieniasy grubas i tak w kółko. Jedyne co dostrzegłem.

wredulus_pospolitus: no i super ... a teraz popatrz na a₃ i a₄. Przypadek 1. 7 x a₃ i 0 x a₄ czy możesz tak złożyć siedem elementów a₃, aby uzyskać 6 'cieniasów' pomiędzy dwoma grubasami

frycek : To skoro kupujemy te 4 przypadki to ten wzór ogólny mógłby wyglądać tak(przynajmniej na początku) a_n=4a_n−1+a_n−2 plus jeszcze ewentualnie tutaj. Ale czy początek jest dobry?

wredulus_pospolitus: Dlaczego tak ma wyglądać a₅ = 4a₄ + a₃ + Z −−−> to da Ci w sumie 4*2 + 1 = 9 GRUBASÓW

frycek : Jeśli bym wziął ten przypadek o którym mówisz wredulusie no to nie mogę, bo użył bym 7 elementów pojedynczych elementów i by było 7 więc żeby było 6 musiałbym zabrać 1

frycek : Czyli w porządku. Czyli dla dla a5 powinno być a5=3a4 + a3 + 1= 3×2 +0 +1=3×2+1=6+1=7

. : Człowieku − nie zgaduj... Motasz cały czas. Napisałem Ci jakie 4 podstawowe przypadki należy rozpatrzeć. Ty zamiast się za to zabrać to wymyślasz inne przypadki

. : 11.30 − − − czyli że względu na liczbę 'cieniasow' pomiędzy dwoma grubasa mi, nie można użyć samych elementów a₃ do utworzenia sekwencji w elemencie a₅. No dobra, w takim razie ten przypadek odrzucamy. Dajesz kolejny przypadek i czekam na Twoja argumentację. Później kolejny i kolejny. Czekam na wniosek i dalsze rozumowanie.

frycek : Czyli przypadek 7a3+0a4 idzie do kosza?

. : Tak... Ponieważ nie możesz stworzyć 6 cienkich pod rząd pomiędzy dwoma grubasami

frycek : A gdyby dać 7 cieniasów tylko zabrać 1 żeby było 6?

. : Keee? Ale co dać 7 cieniasow? Wysławiać się pełnymi zdaniami! Czy przestudiowales wszystkie przypadki które podałem?

frycek : No to ten przypadek jest teraz 5a3 + 1a4 Tutaj też wychodzi 7 5×1+1×2=5+2=7 To teraz pytanie czy mogę użyć 5 elementów a3 i 2 a4 aby było 6 cieniasów pomiędzy 2 grubasami?

frycek : No tak czy nie? I w zasadzie można rozpatrywać w ten sposób każdy przypadek i będzie wychodzić 7czyli o 1 za dużo. Tak na szybko analizując

. : Chłopie... Ty nie rozumiesz. Każdy z tych czterech przypadków da nam 7 grubasów. Pod tym kątem te przypadki zostały stworzone. Teraz patrząc na każdy z tych przypadków, patrzymy czy można jakoś połączyć gotowe już przęsła tak aby ok między dwoma grubymi petami znajdowała się odpowiednią liczba cienkich prętów.

. : Po raz kolejny pokazujesz że nie masz pojęcia co się do Ciebie mówi. Co tylko utwierdza mnie w przekonaniu, że dopuki nie załapiesz tego, to nie ma o czym dalej mówić.

frycek : Dobra. Czyli te przypadki które tu wpisałeś 7a3 + 0a4 5a3 + 1a4 3a3 + 2a4 1a3 + 3a4 Ma nam dać łącznie 7 grubasów w a5. I muszę wybrać któryś z tych przypadków tak aby pomiędzy 2 grubasami mieć 6 cieniasów. Powiedz jeśli coś źle zrozumiałem. Inaczej mówiąc muszę tak połączyć elementy z a3 i a4 żeby otrzymać to co mam w a5 czyli 2 grubasy i pomiędzy nimi 6 cieniasów. Czy tak? Czy nadal źle?

wredulus_pospolitus: nie tylko aby mieć 6 cieniasów ... ale aby mieć sekwencję 4,6,4,6,4 cieniasów pomiędzy grubasami

wredulus_pospolitus: Tak ... o to właśnie chodzi

::::: Kropko, niepotrzebnie się irytujesz. To jest zgadywanka, a nie zadanie, a zgadywania trudno się nauczyć.

. : Z jednej strony masz rację, ale obawiam się że te zadania są dane studentom informatyki, a informatycy powinni bez większych problemów podchodzić do takich problemów i umiejętnie to 'rozłożyć na czynniki pierwsze' w logiczny sposob A tutaj widać bardziej studenta ekonomii bądź wręcz jakiejś filologii który jest wyraźnie zagubiony

frycek : @. : no właśnie masz rację. Ja chce się tego nauczyć i chce rozwiązać to zadanie tylko problem polega na tym, że nie mam na codzień styczności z takimi zadaniami, nie rozwiązuje po 100 takich zadań dziennie.

frycek : Dobra to ja jeszcze z innej beczki chciałbym Cię zapytać. Jak konkret ie doszedłeś do tych przypadków. Rozumiem że przez kombinacje. Staram się poznać wszelkie możliwe przypadki. Czy można by utworzyć tu inne przypadki.

Rrg: dobra, mam kolejny przypadek 5a3 + 1a4. Jak wiemy w tym wypadku też dostane 7 bo 5*1+1*2=5+2=7. No i teraz pytanie? Pewnie brzmi ono tak? Czy mogę użyć 5 elementów z a3 i 2 elementy z a4? No to jak mam mieć 6 cieniiasów pomiędzy 2 grubasami no to nie mogę. Bo mam mieć 6 tych elementów a uzyskuje 5 czyli o jeden za mało ale mam 2 elementy z a4. To skoro a3 się nie zgadza bo mam 5 tych elementów to można wykorzystać te 2 z a4 jako 2 grubasy?

frycek: Sorry. Pisze z innego urządzenia i nie zmieniłem nicku.

wredulus_pospolitus: 1. Zauważam, że w a₅ mamy 7 'grubasów'. 2. w a₃ mamy 1 grubasa, w a₄ mamy 2 grubasy 3. W jaki sposób z X*a₃ + Y*a₄ możemy stworzyć 7 grubasów? 4. Oto w jaki sposób −−−> wypisuje te cztery przypadki Dokładnie w taki oto sposób. Innymi słowy −−− chwyciłem się jakiejś danej którą mam (ilość grubasów) i staram się zobaczyć jaka może być zależność pomiędzy poprzedzającymi elementami ciągu w tej kwestii (ilości grubasów) w celu odgadnięcia tejże zależności

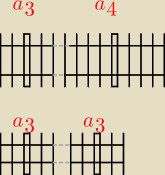
wredulus_pospolitus: Jakim cudem uzyskujesz 5 'cieniasów' "Zespojenie" jednego a₃ z jednym a₄ daje Ci 6 cieniasów pomiędzy dwoma grubasami "Zespojenie" jednego a₃ z jednym a₃ daje Ci 4 cieniasów pomiędzy dwoma grubasami

frycek : Rozumiem. A mogłoby by być np. 2 takie przypadki. Dlaczego akurat 4? Czy to chodzi o to że mamy 5 przypadków z czego żeby dojść do tego piątego musimy pokombinować z tymi wcześniejszymi czterema?

wredulus_pospolitus: co

wredulus_pospolitus: są 4 przypadki bo taka jest liczba rozwiązań równania: x + 2y = 7 dla x,y będących liczbami naturalnymi A teraz pytanie za 100 pkt −−− co studiujesz

frycek : Co studiuję? Jak widać na razie matematykę. I mam parę zaległości, które jak widzę muszę nadrobić.

frycek : A tak na poważnie to interesuje mnie trochę programowanie i postanowiłem trochę pouczyć się rekursji z matmy.

Zaintrygowany: To w końcu jaka jest poprawna odpowiedź do tego zadania?

wredulus_pospolitus: a_n = 3a_n−2 + 2a_n−1 − 2

wredulus_pospolitus: ale szczerze mówiąc −−− nie sprawdzałem innych przypadków które wypisałem (wcześniej doszedłem do tego wzoru, którego potrafiłem 'logicznie wyjaśnić' chociaż nie jestem w 100% zadowolony z wyjaśnienia)

frycek: Dobra, dzięki za wzór, ale chciałbym z waszą(mniejszą bądź większą pomocą) dojść do tego wzoru.

. : A czym był ten wątek jak nie 'większą czy mniejsza' próba na prowadzenia Ciebie na ten wzór?

Jaś: a₁ = 1, a₂ = 2, a₃ = 5, a₄ = 14, a₅ = 40, a₆ = 101, a₇ = 222, a₈ = 435, ... ... , a₁₉ = 25009, a₂₀ = 31370, ...

	1
Ciąg an =		(7n4 − 54n3 + 173n2 − 222n + 120)
	24

. : Jaś − − cudownie tylko: 1. a₅ = 41 (autor źle policzył) 2. Pokaz obliczenia do tegoż wzoru i zmieść się w 10 minutach

Jaś: Nie było mnie przez chwilę. a₁ = 1, a₂ = 2, a₃ = 5, a₄ = 14, a₅ = 41, a₆ = 122, a₇ = 365, ... a obliczenia pozostawiam ciekawskim do samodzielnego wykonania, może za jakiś czas pokażę

Jaś: Minął jakiś czas, więc pokazuję. Nie potrzeba aż 10 minut na zauważenie, że ciąg: 1, 2 = 1 + 3⁰, 5 = 1 + 3⁰ + 3¹, 14 = 1 + 3⁰ + 3¹ + 3², 41 = 1 + 3⁰ + 3¹ + 3² + 3³, ... , a_n = 1 + S_n, gdzie S_n to suma początkowych (n − 1) wyrazów ciągu geometrycznego (a_n), w którym

	3n−1 − 1		1 + 3n−1
a1 = 30, q = 3, zatem an = 1 + 1 *		⇒ an =
	3 − 1		2