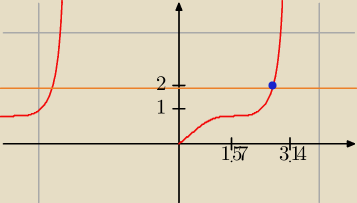
x dla sinus x do potęgi cosinus x równemu 2 sqbi: Hej, ostatnio spotkałem się z dość trudnym równaniem i nie jestem pewien czy dam rady rozwiązać go sam, a sporo czasu nad tym siedze. https://youtu.be/Tf0jetLbFX4 − blackpenredpen rozwiązał sin(x)^sin(x) = 2 używając funkcji W Lamberta, rozwiązanie jest jednak dla liczb zespolonych; sin(x)^cos(x) = 2 ma rozwiązania dla liczb rzeczywistych (jedno z nich zaznaczone niebieską kropką, gdzie y = 2 i y = sin(x)^cos(x) się zderzają), ale nie udało się − ani mu, ani mi − zastosować funkcji Lamberta. Przeszedłem przez wiele tematów matematyki: troche całkowania i pochodnych (nic nie wyszło dobrego), tożsamość eulera (funkcje trygonometryczne jako liczby zespolone, w różnych postaciach), funkcje W Lamberta, funkcje GLOG, logarytmy i dużo dużo nie udanej algebry − ostatecznie wracam do tej samej postaci równania, nic się nie "wyciągło". Wszelkie dostępne kalkulatory ogarniające liczby zespolone, chociażby WolframAlpha, podają jedynie zaokrąglone wartości niektórych rozwiązań (albo wcale nic nie podają, jak MathWay :c ) Najistotniejsze co do tej pory wyciągnałem to: > sin(x) oraz cos(x) mają zbiór wartości od −1 do 1 włącznie, co za tym idzie jedynym wyjściem jest moment, w którym: 0 ≤ sin(x) < ¹₂ i wykładnik będzie ujemny, zatem 0 < cos(x) ≤ −1 ⇒ 0 < sin(x) ≤ ¹₂ ⇔ ≤ π−arcsin(¹₂)+2k*π ≤ x < π+2k*π ⇔ −1 ≤ cos(x) ≤ cos(π−arcsin(¹₂)) dla k ∊ N > Liczne formy tego samego równania: sin(x)^cos(x) = 2 ⇔ (sin²(x))^cos(x) = 4 ⇔ cos(x)*ln(sin(x)) = ln(2) ⇔ (e^ix−e^−ix)^eix+e−ix * (2i)^{−(eix+e−ix)} = 4 ⇔ (csc(x))^eix+e−ix=¹₄ ⇔ sin(x) = 2^1_cos(x) ⇔ sin(x) = 2^sec(x) > Być może zastosowanie funkcji W Lamberta lub GLOG coś wyciągnie: O g(eneralized?)log−u poraz pierwszym usłyszałem tutaj: https://youtu.be/rPAa38VlUUU Funkcja W Lamberta często pada u BPRP, głównie pozwala na obustronne (po prawej najlepiej stałą wartość mieć) zastosowanie W(xe^x) = x Z góry dziękuje za wszelki udział w tym problemie :3

ABC: ale konkretnie o co tobie chodzi? chcesz rozwiązanie z dokładnością do 50 cyfr po przecinku?

sqbi: Żeby znaleźć konkretne rozwiązania, a nie przybliżenia − rozwiązanie w którym po lewej stronie równości mam iksa, a po drugiej stałą wartość rozpisaną jak ma to miejsce u BPRP z sin(x)^sin(x)=2

Mariusz: sqbi a na anglojęzycznych forach nic ci nie pomogli ?

: tam trzeba byś mnichem w siódmym pokoleniu

ABC: ale to i tak są funkcje przestępne , i co ci da to rozwiązanie ? w praktyce inżynierskiej i tak bierze się przybliżenia

sqbi: Później mogę spróbować zadać ten problem na innych forach, jak patrzałem to nikt wcześniej nie opisywał tego − jedynie jakiś mały wątek na Reddicie był, ale tam nikt tego nie tknął. Teraz próbuje rozwiązać to w formie:

	ln(2)
cos(x) =
	ln(sin(x))

	ln(2)
x = arccos(		)
	ln(sin(x))

i szukam definicji arccos w liczbach zespolonych:

	eix+e−ix
y = cos(x) ⇒ y =		| inverse
	2

	eiy+e−iy
x =		| niech z = eiy
	2

	z+z−1
x =		⇔ 2x = z+z−1 ⇔ 2x*z = z2+1
	2

−z² + 2x*z − 1 = 0

	−(2x) ± √ (2x)2 − 4*(−1)*(−1)
z =
	−2

	√4x2−4
z = x ±
	2

z = x ± √x²−1 iy = ln( x ± √x²−1 ) y = ¹_i*ln( x ± √x²−1 ) ⇔ arccos(x) = −i*ln( x ± √x²−1 )

	ln(2)
Więc na to, że x = −i*ln(		± √(ln(2)ln(sin(x)) )2−1)
	ln(sin(x))

Może z tego da się coś wyciągnąć

sqbi: ABC − satysfakcje mi to da Wiem, że to wszystko wychodzi jako transcendalne liczby − zarazem można je wyrazić za pomocą funkcji W Lamberta czy innymi środkami zrobić wynik ładnym.

ABC: jak tak chcesz się bawić , to nie lepiej szukać rozwiązań układu : x²+y²=1 , y^x=2 , gdzie x=cost, y=sint i najpierw znaleźć wartość a potem argument? drugie można zlogarytmować x*lny=ln2 i coś podobnego wychodzi jak u ciebie ale prostsze rachunki

sqbi:

⎧	x2 + y2 = 1
⎩	yx = 2	gdzie x = cos(t), y = sin(t)

	ln(2)
yx = 2 ⇔ x*ln(y) = ln(2) ⇔ x =
	ln(y)

	ln(2)		ln(2)2
(		)2 + y2 = 1 ⇔		+ y2 = 1
	ln(y)		ln(y)2

	ln(2)2+y2*ln(y)2
⇔		= 1
	ln(y)2

I co teraz?

ABC: kombinuj z funkcją lamberta może coś wyjdzie

Mariusz: " tam trzeba byś mnichem w siódmym pokoleniu ," Coś w tym jest bo tam bezpodstawnie usuwają/zamykają wątki Może dlatego nie chciał tam zadawać pytań bo wnosząc z tego że ogląda filmiki po angielsku to z językiem nie ma problemów

sqbi: @Mariusz, właściwie to nie znam innych forów matematycznych, a tutaj już jakiś czas temu sie pojawiałem. Jeśli wciąż nie rozwiąże tego, to będe szukał dalej rozwiązania.

sqbi: Starałem się zastosować równanie kwadratowe do:

(ln 2)2
	+ y2 − 1 = 0 ⇔ (ln y)2y2 − (ln y)2 + (ln 2)2 = 0
(ln y)2

ale raczej to zbyt dobrze nie funkcjonuje z zmiennymi współczynnikami a i c, nic ciekawego też nie wyciągnąłem; zakładając, że b = 0 i c = −(ln y)²+(ln 2)² udało mi się dostać delte: Δ = (2(ln y)²)*( 2(ln y)² − 2(ln 2)² ) − pomimo tego, że da się wykalkulować jedyne rozwiązanie y ≈ 0.458437, to zakładając Δ = 0 dostaje się sprzeczne wyniki i trudno jest to zgrać ze sobą − dalsza algebra po podstawieniu delty zwraca poprzednią forme równania Zatem pada pytanie − jak wcisnąć zmienny współczynnik w równanie kwadratowe albo jakie inne równanie możnaby zastosować? Zastanawiam się też nad tym, czy z równań podobnych do kwadratowego, takich jak: a(ln(x^x))⁻² + bx⁻² + c = 0 ax² + bx²ln(x^x) + c = 0 a(x ln x)² + b(ln x)² + c = 0 ax² + b(ln x)⁻² + c = 0 − gdzie a, b i c miałyby być współczynnikami danego równania − dałoby się stworzyć ładny wzór na x

	(ln 2)2
(podane równania to przekształcone równanie		+ y2 − 1 = 0 więc jeśli
	(ln y)2

istnieją takie typy równań podobne do kwadratowego, bez problemu dałoby się podstawić współczynniki)

sqbi: Innymi słowy, z równania (ln y)²y² − (ln y)² + (ln 2)² = 0 dzięki podstawianiu można zrobić funkcje liniową czy kwadratową z zmiennym współczynnikiem: (ln y)²y² − (ln y)² + (ln 2)² = 0 | Niech u = (ln y)² u = (ln y)² ⇒ ln y = √u ⇒ y = e^√u ⇒ y² = e^2√u ue^2√u − u + (ln 2)² = 0 u(e^2√u − 1) + (ln 2)² = 0 (ln y)²y² − (ln y)² + (ln 2)² = 0 | Niech u = ln y u = ln y ⇒ y = e^u ⇒ y² = e^2u u²(e^2u − 1) + (ln 2)² = 0 so how do you deal with that now, hmm? Co psuje ten zmienny współczynnik?

Mariusz: A jak dostałeś to przybliżenie y ≈ 0.458437,

sqbi: @Mariusz, to już WolframAlpha oszacował, pewnie użył metody Newtona czy czegoś w tym stylu

Mariusz: Ja jak to zadanie pierwszy raz zobaczyłem to jedynie pozbyłem się funkcji trygonometrycznych bawiąc się podstawieniem Eulera i jedynką trygonometryczną i już dalej się nie bawiłem

pr: https://www.wolframalpha.com/input?i=sinx%5Ecosx+%3D+2

123: tylko dlaczego x = i w rozwiązaniu jest coś z x

123: nie było pytania....

sqbi: @pr WolframAlpha zbadałem wszerz i wzdłuż, i jedyne co potrafi wypluć to rozwiązania numeryczne

sqbi: Po milionach prób i łez wróciłem spowrotem do pochodnych: sin(x)^cos(x) = 2

d
	sin(x) = cos(x) ⇒ sin(x)ddxsin(x) = 2
dx

^d_dxsin(x) ln(sin(x)) = ln 2 tutaj mi się zaświeciła lampka − prawdopodobnie gdzieś tutaj można zrobić Lambertem wyodrębnienie, Wolfram Alpha też sie ze mną zgadza: https://imgur.com/a/kzdVDHs Musze się doedukować w kwestii tych ODE, może to pomoże w znalezieniu analitycznego rozwiązania

Min. Edukacji: z powrotem🤪

sqbi: Przepraszam Ministrancie Edukacji ^d_dx sin(x) * ln(sin(x)) = ln 2 ∫^d_dx sin(x) * ln(sin(x)) dx = ∫ ln 2 dx ∫^d_dx sin(x) * ln(sin(x)) dx = ln(sin(x)) * sin(x) − ∫ cot(x) sin(x) dx ∫ cot(x) sin(x) dx = sin(x), ∫ ln 2 dx = x ln 2 ln(sin(x)) * sin(x) − sin(x) = x ln 2 + C sin(x) (ln(sin(x)) − 1) = x ln 2 + C

	sin(x)
ln(sin(x)) − 1 = ln(sin(x)) − ln(e) = ln(		)
	e

	sin(x)
sin(x) ln(		) = x ln 2 + C
	e

sin(x)		sin(x)		x ln 2 + C
	ln(		) =
e		e		e

	sin(x)		x ln 2 + C
eln(sin(x)e) ln(		) =
	e		e

	x ln 2 + C
ln(sin(x)e) = W(		)
	e

Wracając do tej postaci z pochodną − jest jeden problem: Pozostanie i tak po obu stronach zmienna oraz stała całkowania po prawej jeśli użyje sie obustronnego całkowania, więc nie wiem czy da się to potem jakoś zintegrować tak by wydzielić na jedną strone zmienne Sama postać bardzo ładnie wygląda, prawie jak sama definicja właśnie funkcji W Lamberta...

Mariusz: "Musze się doedukować w kwestii tych ODE" Poważnie chcesz się tym zająć ? W ostatnim wpisie poniższego wątku będziesz miał spis tematów którymi można by się zająć https://matematykaszkolna.pl/forum/385133.html Pewnie do tego spisu można by coś dopisać jednak ja czytałem o ODE samodzielnie Nie miałem ich w szkole