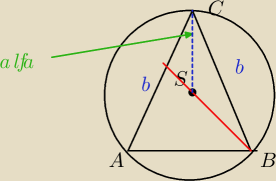
Planimetria silnia: W trójkącie równoramiennym ostrokątnym ABC mamy dane |AC | = |BC | = b oraz |∡ACB | = α . Z wierzchołka B przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok AC w punkcie D . Oblicz promień okręgu wpisanego w trójkąt ABC oraz długość odcinka BD.

	α
ΔBSC − równoramienny, kąt przy B i C to
	2

Dalej nie wiem jak to ruszyc

ite: Mało ambitnie ale wygodnie: 1/ promień okręgu wpisanego w trójkąt ABC oblicz ze wzoru podanego https://matematykaszkolna.pl/strona/542.html 2/ długość odcinka BD z tw. sinusów dla ΔCBD

silnia: W sumie to trzeba policzyc tylko |BD|, tylko skopiowalem polecenie

ite: Określ miary kątów w ΔCBD i skorzystaj z tw. sinusów dla tego trójkąta.

silnia: α, ^α₂, 180deg − ³₂α, tak? Koxem z planimetrii i dowodow nigdy nie bylem, stad moze dlatego moje glupie pytania

ite: dokładnie takie kąty, a to że ktoś pyta, to na tym forum zupełnie normalne : )

silnia: No okej, czyli

b		BD
	=2R=
sin32α		sinα

?

www: https://zadania.info/d645/9092733