Planimetria dowodzenie PR silnia: Wykaż, że środki boków dowolnego czworokąta wypukłego tworzą równoległobok o obwodzie mniejszym niż obwód tego czworokąta.

wredulus_pospolitus: to że obwód będzie mniejszy − to chyba logiczna logiczność ... więc trzeba tylko tak naprawdę pokazać, że będzie to równoległobok

mat: https://matematykaszkolna.pl/forum/396304.html

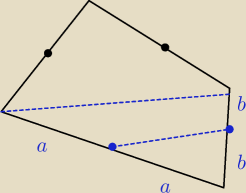
wredulus_pospolitus: zauważ, że mamy tutaj:

a		2a
	=		<−−− tw. Talesa
b		2b

ergo −−− te dwa odcinki są równoległe ... analogicznie z górną częścią ... następnie zauważamy, że jeden z odcinków jest wspólny dla obu wariantów (przekątna wyjściowego czworokąta). ergo −−− wszystkie te trzy odcinki są równoległe. Analogicznie 'pionowe' odcinki. i gotowe.