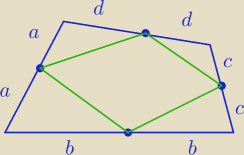
Łączenie środków dowolnego czworokąta i dowód Kamil: Wykaż, że środki boków dowolnego czworokąta wypukłego tworzą równoległobok o obwodzie mniejszym niż obwód tego czworokąta. Zdołałem udowodnić, że środki boków czworokąta tworzą równoległobok. Nie wiem tylko jak udowodnić, że obwód powstałego równoległoboku jest mniejszy od obwodu czworokąta. Myślałem o twierdzeniu kosinusów, ale nic z tego sensownego mi nie wyszło. Byłbym wdzięczny za podpowiedź

ite: Skorzystaj z nierówności trójkąta dla trójkątów wyciętych przez zielone odcinki.

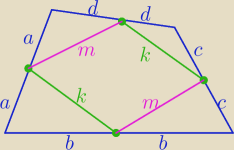
Eta: a+b>k c+d>k b+c>m a+d>m + −−−−−−−−−−− 2(a+b+c+d)>2(k+m) L > L₁ L₁ < L

Kamil: No właśnie wyszedłem na spacer i wpadłem na pomysł, żeby skorzystać z tej nierówności trójkąta Dziękuję za pomoc