Zadanie na dowodzenie z trójkątem dowolnym i okręgiem wpisanym Althea: Witam. Liceum ogólnokształcące, rozszerzenie. Mam problem z zadaniem: Niech O oznacza środek okręgu wpisanego w trójkąt ABC. Prosta AO przecięła bok BC w punkcie M. Długości boków trójkąta ABC są równe a=|BC|, b=|CA|, c=|AB|.

	|AO|		b+c
Udowodnij, że		=		.
	|OM|		a

Althea: A, zapomniałam dodać. Prawdopodobnie jest z tego samego zbioru co ten wpis: https://matematykaszkolna.pl/forum/416584.html Niestety nie mam dostępu do samego zbioru.

chichi:

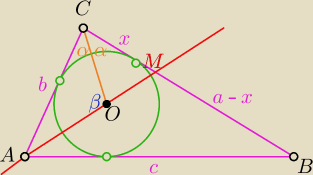
	a − x		c		ab
(1) z tw. o dwusiecznej mamy, że:		=		⇔ x =
	x		b		b + c

(2) niech |∡AOC| = β ⇔ |∡COM| = 180^o − β

	|AO|		b
(3) z tw. Snelliusa w ΔAOC mamy, że:		=		⇔
	sin(α)		sin(β)

	bsin(α)
⇔ |AO| =
	sin(β)

	|OM|		x
(4) z tw. Snelliusa w ΔCOM mamy, że:		=		⇔
	sin(α)		sin(180o−β)

	xsin(α)
⇔ |OM| =
	sin(β)

zatem mamy:

|AO|		bsin(α)		sin(β)		b		b + c
	=		*		=		= b *		=
|OM|		sin(β)		xsin(α)		x		ab

	b + c
=		. □
	a

chichi: teraz tak patrzę na swój rysunek i widzę, że szybciej można przeprowadzić ten dowód pomijając 2,3 i 4 podpunkt − stosując drugi raz tw. o dwusiecznej dla trójkąta AMC, mamy:

|AO|		b		ab
	=		, teraz tak samo kładziemy x =		z (1) i mamy tezę
|OM|		x		b + c