stereometria zasady weyo: chciałbym poznać zasady ze stereometrii na mature których nie ma w tablic a które trzeba znać żeby rozwiązywać zadania na maturze. Mam kilka i mam pare pytan o nie i czy trzeba znac cos jeszcze 1) W ostrosłupach prawidłowych środek okręgu opisanego na podstawie pokrywa się ze środkiem okręgu wpisanego w podstawę i jest spodkiem wysokości ostrosłupa. Czy to jest wazne? 2)Jeżeli w ostrosłupie wszystkie krawędzie boczne są równe lub są tak samo nachylone do płaszczyzny to spodek wysokości znajduje się w środku okręgu opisanego na podstawie. 3) Jeżeli w ostrosłupie wszystkie ściany boczne są nachylone pod tym samym kątem do płaszczyzny podstawy to spodek wysokości znajduje się w środku okręgu wpisanego w podstawę. rozumiem ze roznica miedzy 2 a 3 ze jedna to sciany druga to krawedzie i wtedy inaczej to sie opisuje srodek. mam jeszcze ze jezeli wszystloe wysokosci scian bocznych w ostroslupie sa rowne to w podstawie mozna wpisac okrag i srodek okregu jest spodkiem wysokosci czy to wszystko sie zgadza i nie walnalem jakiegos bledui czy kazdy z tych twierdzen fakyucznie trzeba wykuc na pamiec na mature? Czy jest moze jakas metoda albo nie wszystkie? Czy jest cos moze jeszxze waznego?

wredulus_pospolitus: odnośnie (3) to jeszcze analogicznie do (2) można napisać: "Jeżeli w ostrosłupie wszystkie krawędzie boczne są równe lub są tak samo nachylone do płaszczyzny lub wysokości ścian bocznych są sobie równe to spodek wysokości znajduje się w środku okręgu opisanego na podstawie."

weyo: to jest to samo co napisalem tam na koncu nie w sensie tu mam jeszcze ze jezeli wszystloe wysokosci scian bocznych w ostroslupie sa rowne to w podstawie mozna wpisac okrag i srodek okregu jest spodkiem wysokosci

weyo: ale tak wlasciwie to skąd to bierzecie? Czy faktycznie trzeba to wykuć na pamięć?

weyo: a jaka jest roznica miedzy nachyleniem sciany bocznej a krawedzi

wredulus_pospolitus: wynika z tego, że: 2) w przypadku okręgu opisanego na podstawie −−− punktami styczności okręgu i podstawy będą wierzchołkami podstawy. Budujemy zatem n trójkątów prostokątnych (dla każdego z wierzchołków podstawy) zawierający: wierzchołek podstawy, krawędź boczną ostrosłupa, wysokość ostrosłupa. 2 z trzech boków jest zawsze sobie równa. Są to trójkąty prostokątne, więc cechą BBK mamy przystawanie tych trójkątów, więc kąty są równe (krawędzie boczne nachylone pod tym samym kątem), oraz trzeci bok (odległość krawędzi od spodka wysokości) jest równy w każdym przypadku. Natomiast punkt który jest równoodległy od wszystkich wierzchołków to nic innego jak środek okręgu opisanego na tejże podstawie. 3) analogiczne rozumowanie, tylko należy pamiętać że punkty styczności okręgu z krawędziami podstawowymi będą tam skąd poprowadzone będą wysokości ścian bocznych

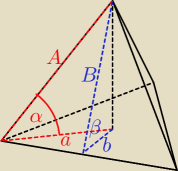
wredulus_pospolitus: zasadnicza różnica jest pomiędzy kątami A > B ; a > b ... α < β

weyo: ale nie rozumiem bo ja mialem zapisane z lekcji ze jak wysokosci scian bocznych sa rowne to okrag mozna wpisac do podstawy a ty tu piszesz ze mozna opisac to jak to jest?

mati: https://matematykaszkolna.pl/forum/191409.html

weyo: tak znam ten post i z niego tez korzystalem ale o wysokosci scian bocznych tam nie ma

weyo: czy srodek jest w okregu wpisanym czy opisanym