pytanie o spodki
tn: Witam,
Gdzie leży spodek wysokości w następujących ostrosłupach:
ostrosłupie o podstawie:
trapezu
trapezu równoramiennego
równolegloboku
rombu
prostokątu?
Czy jeżeli wszystkie krawędzie są nachylone pod tym samym kątem do podstawy to czy krawędzie są
tej samej długości?
10 mar 16:53
10 mar 18:51
10 mar 19:03
tn: no tak, ale jakieś ogólne fakty istnieją?
\
10 mar 20:00
Mila: Po kolacji, parę zasad podam.
10 mar 20:03
tn: ok, ok
10 mar 20:09
Mila:
1) W ostrosłupach prawidłowych środek okręgu opisanego na podstawie pokrywa się ze środkiem
okręgu wpisanego w podstawę i jest spodkiem wysokości ostrosłupa.
2) Jeżeli w ostrosłupie wszystkie krawędzie boczne są równe to spodek wysokości znajduje
się w środku okręgu opisanego na podstawie.
3)Jeżeli w ostrosłupie wszystkie krawędzie boczne są nachylone pod tym samym kątem do
płaszczyzny podstawy to spodek wysokości znajduje się w środku okręgu opisanego na
podstawie.
4) Jeżeli w ostrosłupie wszystkie ściany boczne są nachylone pod tym samym kątem do
płaszczyzny podstawy to spodek wysokości znajduje się w środku okręgu wpisanego w
podstawę.
10 mar 20:48
henio: ok, dziękuję
A czy np. w rombie nie jest tak, że tak jak w kwadracie− na przecięciu się przekątnych? ( albo
w równoległoboku)
10 mar 21:14
Mila: Jeśli w treści podane, że ściany boczne są nachylone pod tym samym kątem do płaszczyzny
podstawy ( rombu) to spodek wysokości znajduje się w środku okręgu wpisanego w podstawę, czyli
na przecięciu przekątnych.
Z równoległobokiem w podstawie, to inne zagadnienie.
10 mar 21:20
henio: Ok, czyli jako tako nie ma punktów charakterystycznych. Dopiero jak nam powiedzą, że krawędzie
mają taką samą długość itp. to wtedy możemy się zastanawiać.
Czy tak?
10 mar 21:33
Mila: W zadaniach zwykle jest sprecyzowane położenie spodka wysokości ostrosłupa lub jeden z 4
podanych przypadków.
10 mar 21:48
henio: Dzięki!
10 mar 22:05
Mila:
10 mar 22:07
henio: czy jeżeli mamy w zadaniu dany graniastosłup niepochyły to czy zawsze krawędzie są pod kątem
prostym do podstawy?
11 mar 00:09
henio: bo jakbyśmy rzutowali, to gdzie się pojawią punkty?
11 mar 00:11
Mila:
W graniastosłupie prostym ściany boczne ( krawędzie boczne też) są prostopadłe do płaszczyzny
podstawy.
11 mar 15:43
henio: dzięki
sześcian o krawędzi długości 3 przecieto płaszczyzną przechodzącą przezs prezkątną podstawy i
tworząca z płaszczyzną kąt α. oblicz pole otrzymanego przekroju dla:
a) α=45
<a href="
http://imgur.com/C7dy1rW"><img src="
http://i.imgur.com/C7dy1rW.png" alt="" title="Hosted by imgur.com" /></a>
Popatrzcie na rysunek. Ktoś pokazał dwa sposoby oznaczenia kąta pomiędzy przekrojem a podstawą.
Czy oba są poprawne i dlaczego oba są poprawne? ( lub dlaczego nie są?)
11 mar 20:21
dero2005:
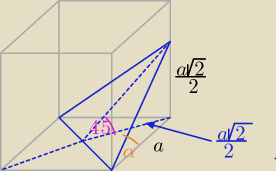
α<45
o
11 mar 20:59
henio: ok, dzięki
Żeby stwierdzić, że prosta jest prostopadła do płaszczyzny musimy pokazać, że ta prosta jest
prostopadła do dwóch prostych w płaszczyźnie?
11 mar 21:57
Mila:
Z kątem ładnie Dero wyjaśnił.
Jeżeli prosta przebija płaszczyznę i jest prostopadła do płaszczyzny, to jest prostopadła do
każdej prostej leżącej w tej płaszczyźnie i przechodzącej przez punkt przebicia.
Narysuj pęk prostych na kartce i zilustruj sytuację, możesz ustawić ołówek w punkcie przebicia
i wczytaj się w to co napisałam.
Jeśli to zrozumiesz, to będzie pomocne.
11 mar 22:53
