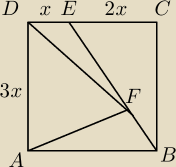
W kwadracie ABCD punkt E dzieli bok CD w stosunku 2:1 licząc od wierzchołka C mak: Proszę o pomoc! W kwadracie ABCD punkt E dzieli bok CD w stosunku 2:1 licząc od wierzchołka C . Na odcinku BE obrano taki punkt F , że |AD|=|DF| . Oblicz, jaką część pola kwadratu ABCD stanowi pole trójkąta AFD.

an:

	4√3+3
sin(α+β)=
	13

	9		4√3+3
PAFD=
	2		13

mak:

	4√3+3
Nie do końca rozumiem skąd pojawiły się te liczby. A odpowiedz powinna wyjść		.
	26

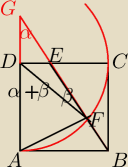
an: Podałem pole trójkąta, które należy podzielić przez pole kwadratu, można to zrobić na paluszkach zaznaczyłem kąty których sin można wyznaczyć a następnie przez wzory otrzymać sin(α+β), ale niestety trzeba trochę pomyśleć popracować

mak: Przepraszam, ale jak można wyznaczyć te sinusy? Już mi się śni po nocach to zadanie...

an: czy masz problem z sinα ?⇒ to podstawy sinβ ⇒twierdzenie sinusów

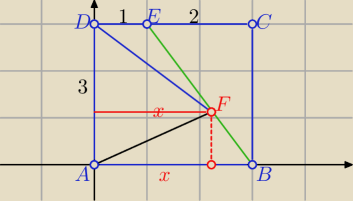
Eta: Można też analitycznie bez straty ogólności: D(0,3) , B(3,0), E(1,3)

	3		9
prosta EB ma równanie : y= −		x+
	2		2

	3		9		3		9
to F(x, −		x+		) |DF|=√x2+(−		x+		−3)2
	2		2		2		2

	1
P(AFD)=		*3*xF
	2

	3		3
|DF|2= 9 to x2+(−		x+		)2
	2		2

.................... 13x²−18x−27=0 i x>0

	9+12√3
Δ=....... x=
	13

	1		9+12√3
PΔ(ADF)=		*3*		i P□=9
	2		13

PΔ		3+4√3
	=
P□		26

==========

Mila: mak, jeżeli interesuje Cię rozwiązanie z zastosowaniem trygonometrii, to wpiszę. Rozwiązanie w układzie wsp. jest prostsze, kiedyś Janek też gdzieś na forum podobnie rozwiązał.

Eta: https://matematykaszkolna.pl/forum/409756.html

silnia: 13x2−18x−27=0 i x>0 Rownanie kwadratowe jest dobre? Mi wychodzi 13x2−18+9=0 i x>0

Mila: Zobacz w linku podanym przez Etę 21:16 tam są szczegółowe obliczenia. Równanie Ety jest "dobre".