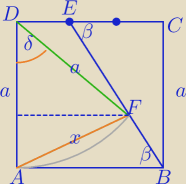
olanimetria dzonypieczony: W kwadracie ABCD punkt E dzieli bok CD w stosunku 2:1 licząc od wierzchołka C . Na odcinku BE obrano taki punkt F , że AD = DF . Oblicz, jaką część pola kwadratu ABCD stanowi pole trójkąta AFD . sorka że tak spamie tymi zadaniami ale po prostu czas mnie goni jak ktoś by mi mógł tylko pokazać jak je zrobić to już dużo mi daje

dzonypieczony: problem mam z obliczeniem pola DEF oraz FAB

chichi: Zrozumieć rozwiązanie, to żadna sztuka, ale samemu na nie wpaść i je rozwiązać, to już tak. Lepiej jak sam usiądziesz i pogrzebiesz przy samodzielnych rozwiązaniach nawet mniejszej ilości zdań, niż oczytasz się dziesiątek rozwiązanych przez innych

ICSP: Nie do końca. Pamiętam, że rozwiązanie tutaj przez Ete jednego zadania z planimetrii uratowało mi 2 punkty na maturze podstawowej.

chichi: Co nie zmienia faktu, że gdybyś posiedział nad zadaniem dłużej i sam je rozwiązał − pomógłbyś sam sobie

dzonypieczony: chichi zgadzam sie z tobą, aczkolwiek czas mi nie pozwala na takie przyjemności, a chcę jak najwięcej zadań przerobić

dzonypieczony: a jeszcze geometria analityczna i stereometria mi została do przerobienia

chichi: No co nie zmienia faktu, że trzymam kciuki. Co mogę doradzić, to może zamiast wrzucać nowe zadania i czekać na rozwiązania, skorzystaj już z dziesiątek tysięcy zadań rozwiązanych z tych działów, tutaj na forum czy zadania.info czy matematyka.pl

dzonypieczony: ja wrzucam te ktorych nei wiem jak zrobic i kombinuje z nastepnymi ale dzięki w kazdym razie

dzonypieczony: a jakies wskazowki chociaz na co patrzeć w tym zadaniu xd

Mila:

1   a2sinδ 2		1
	=		sinδ
a2		2

Mila: Policzyłam dalej , ale wynik mi się nie podoba. Do jutra

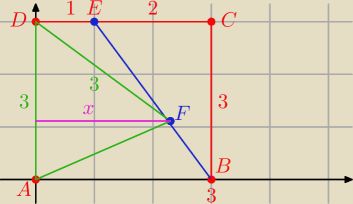
janek191: pr. BE

	3		9
y = −		x +
	2		2

więc

	3		9
F = ( x, −		x +		)
	2		2

I DF I = 3

	3		9
I DF I2 = x2 + ( 3 − (−		x+		)2) = 9
	2		2

	3		3
x2 + (		x −		)2 = 9
	2		2

	9		9		9
x2 +		x2 −		x +		= 9 / 4
	4		2		4

4 x² + 9 x² − 18 x + 9 = 36 13 x² −− 18 x − 27 = 0 Δ = 1728 = 16*36*3 √Δ = 24 √3

	18 + 24 √3		9 + 12 √3
x =		=
	26		13

	13,5 + 18 √3
PΔ{AFD} = 0,5*3*x =
	13

P_ABCD = 3² = 9 zatem

	13,5 + 18 √3		27 + 36√3
U{ PΔ{AFD}}{PABCD =		=
	13*9		234

janek191:

	27 + 36 √3
PΔAFD : PABCD =
	234

Mila:

	3+4√3
1) sinδ=
	13

	[AFD]		3+4√3
2)		=
	[ABCD]		26

Mila: Wynik jak u Janka