okrag wpisany gibby: W trójkąt równoramienny ABC AC=BC wpisano okrąg.Punkt D jest punktem styczności tego okręgu z ramieniem BC i dzieli to ramie na odcinki długości BD=5 i CD=3. Oblicz AD Próbowałam z pól (z Herona) P.abc = √13*3*5*5 = P.abd + P .acd ale rachunki wychodzą potworne i zastanawiam się czy to wgl dobry sposób i warto w to brnąć

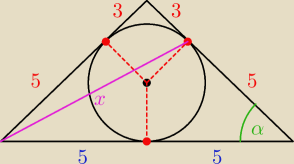
wredulus_pospolitus: z tw. cosinusów:

	5
82 = 82 + 102 − 2*8*10*cosα ⇔ 16cosα = 10 ⇔ cosa =
	8

no to teraz: x² = 5² + 10² − 2*5*10*cosα podstawiasz i gotowe

wredulus_pospolitus: PS. Oczywiście wartość cosα można było wyznaczyć z trójkąta prostokątnego po narysowaniu wysokości

www: https://matematykaszkolna.pl/forum/368916.html

gibby: kurczę rzeczywiście, dzieki wielkie

wredulus_pospolitus: a tak przy okazji −−− wzór Herona jest supcio dupcio, ale w szkole nie ma praktycznie zadań które by wymagały skorzystanie z niego

chichi: czasami pojawiają się zadania, aby obliczyć pole trójkąta mając podane dłg. 3 boków, niektórzy z tw. Carnota wyznaczają wartość cosinusa jednego z kątów, później z 1 tryg. wartość sinusa

	1
tego kąta i liczą pole ze wzoru S =		absin(α), ale można inaczej − posłużyć się właśnie
	2

Heronem