Poprawna wersja wcześniejszego zadanie Halinka : Dany jest Δ abc. Bok AC=5 a bc= 4. Kat leżący naprzeciw boku ab jest dwa razy większy od kąta naprzeciw bc Obliczyć długość boku AB

Pitbull puppies forever:

	√7
jesli kąt przy wierzchołku A nazwać α to po pewnych rachunkach sinα=
	4

potem wyliczyc sin2α itd.

Milena: a skad ten pierwiastek

chichi: https://matematykaszkolna.pl/forum/416130.html spojrzałaś w ogóle do wątku, w którym wrzuciłem rozwiązanie czy o co tu chodzi

Milena: Tak i teraz to już zupełnie sie pogubiłam

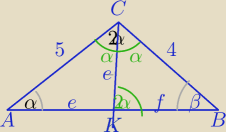
Mila: Z kilku rozwiązań podaję jedno: CK− dwusieczna kąta C 1) Z tw o dwusiecznej kąta:

e		5		5
	=		⇔e=		f
f		4		4

	9
|AB|=e+f=		f
	4

2) ΔCKB∼ΔABC

4		KB
	=		⇔ |AB|*|KB|=16
AB		4

9		4*16
	f*f=16 ⇔ f2=
4		9

	8		10
f=		, e=
	3		3

|AB|=6 =====

Halinka: Mila dziękuje. W pewnym momencie stanęłam

Mariusz: W tamtym wpisie Halinka miała dobry pomysł na rozwiązanie tego zadania i nie wiem czemu się poddała Jeżeli twierdzenie cosinusów to dwa razy Pomysł chichiego może nawet lepszy ale wymagał dorysowania pewnego trójkąta i zauważenia podobieństwa trójkątów a z tym bywa różnie tzn nie każdy jest w stanie wpaść na to co dorysować itp tym bardziej że w szkole bardziej kładą nacisk na wykorzystanie wzorów takich jak twierdzenie cosinusów

chichi: moje rozw. było bardziej do załapania dla początkujących konkursowiczów

Mila: Początkujący konkursowicz może też skorzystać z tw. Stewarta. Rys. z 16:4

	e		5
1)		=		− z tw. o dwusiecznej
	f		4

	5
f=		e
	4

5²*f+4²*e=(e+f)*(|CK|²+e*f), |CK|=e dalej praca dla kaszojadki

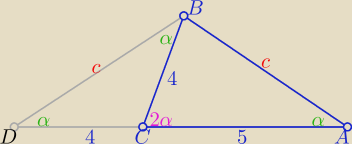
Eta: Z podobieństwa trójkątów równoramiennych ADB i DCB ( kkk)

	c		4
		=		⇒ c2=36
	9		c

c= |AB|=6 i po ptokach

Mila: Tak rozwiązał chichi

Eta: Sorry nie widziałam ( to w następnym linku)

Mila: To przecież żaden problem. Rysunek piękny. Łatwo ułożyć proporcję.