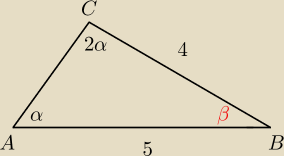
Od czego zacząć Halinka : Dany jest Δ abc. Bok AC=5 a bc= 4. Kat leżący naprzeciw boku ab jest dwa razy większy od kąta naprzeciw bc

Halinka : Obliczyć długość Ab. Tw. Cosinusów?

Saizou : A co masz obliczyć? Z tw. sinusów

5		4
	=
sin(2α)		sinα

4*sin(2α) = 5*sinα 4*2sinαcosα = 5*sinα /:sinα 8cosα = 5

	5
cosα =
	8

β = 180−3α cos(180−3α) = cos(3α) = 4cos³α−3cosα

chichi:

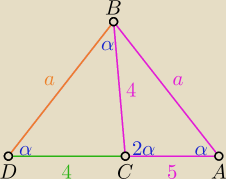
	a		4
ΔADB ∼ ΔDCA (cecha k−k−k) ⇒		=		⇒ a2 = 36 ⇒ a = 6
	9		a

P.S. rysunek jest tylko poglądowy, miary nie są zachowane.

Halinka : Trzeba policzyć długość boku AB

Mila: Popraw zapis : "ΔDCA" .

Mariusz: DCA to trójkąt zdegenerowany ADB∼CDB Saizou tutaj źle oznaczył długości boków Halinka "Obliczyć długość Ab. Tw. Cosinusów?" Tutaj trzeba by było ułożyć dwa równania z twierdzenia cosinusów i dostaniemy wtedy układ równań który sprowadza się do rozwiązania równania dwukwadratowego x² = 5²+4²−2*4*5cos(2α) 16 = x²+25 − 2*5*xcos(α) x² = 41 − 40cos(2α) −9 = x² −10xcos(α) 10xcos(α) = x²+9 x² = 41 − 40(cos²(α)−sin²(α))

	x2+9
cos(α) =
	10x

x² = 41 − 40(cos²(α)−(1−cos²(α)))

	x2+9
cos(α) =
	10x

x² = 41 − 40(2cos²(α)−1)

	x2+9
cos(α) =
	10x

x² = 81 − 80cos²(α)

	(x2+9)2
x2 = 81−80(		)
	100x2

	x4+18x2+81
x2 = 81−80
	100x2

	x4+18x2+81
x2 = 81−4
	5x2

5x⁴ = 405x² − 4(x⁴+18x²+81) 5x⁴ = 405x² − 4x⁴−72x²−324 9x⁴−333x²+324 =0 x⁴ − 37x² + 36 = 0 t = x² t² − 37t + 36 =0 (t−1)(t−36)=0 Teraz x=1 należy odrzucić bo nie spełnia nierówności trójkąta

chichi: @Mila nie poprawię, zostawię to dla autora. rzecz jasna wkradł się chochlik, dzięki za czujność

Mila: chichi Rozwiązanie piękne Krótkie.

Mariusz: Twierdzenie cosinusów to był oryginalny pomysł Halinki a dodatkowo łatwo na niego wpaść i działa Gdybyśmy po obliczeniu x sprawdzali także wartość cos(α) to nie trzeba by było korzystać z nierówności trójkąta

ABC: Mariusz pięknie, właśnie mnie niedawno pytali uczniowie do czego im się mogą przydać równania dwukwadratowe w innych działach matematyki

Mariusz: I co im powiedziałeś ? Zaglądałeś do tematu https://matematykaszkolna.pl/forum/416112.html Chodzi o uzasadnienie że

	δn		dn
		ex2e−(t−x)2|t=0 = (−1)nex2		e−x2
	δtn		dxn

i sposób na policzenie tej pochodnej

ABC: no brakowało mi przykładów a teraz mam twój takimi równaniami różniczkowymi to ja się już od wielu lat nie zajmuję