Oblicz promień okręgu wpisanego w trapez
Kuchin: Oblicz promień okręgu wpisanego w trapez o podstawach długości 18cm i 22cm. Warto zauważyć że w
zadaniu nie jest napisane, że trapez ten ma być równoramienny. Nie mam pojęcia jak rozwiązać
to zadanie w takim wypadku.
9 paź 21:26
9 paź 23:12
wredulus_pospolitus:
@mat −−− tyle że wskazana przez Ciebie wersja jest dla trapezu równoramiennego
9 paź 23:36
Kuchin: @mat Dzięki, widziałem już to rozwiązanie, sęk w tym że mam za zadanie policzenie dokładnie
tego zadania, lecz bez założenia że trapez jest równoramienny.
9 paź 23:38
wredulus_pospolitus:
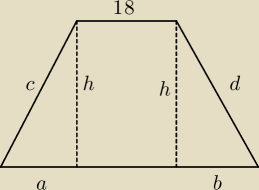
a+b = 2
c+d = 18+20 = 38
a
2 + h
2 = c
2
b
2 + h
2 = d
2
a tak naprawdę to jest tylko jedna (mniej skomplikowana) z dwóch możliwości
9 paź 23:42
wredulus_pospolitus:
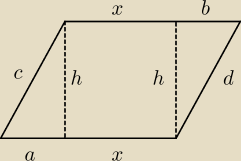
a+x = 20
b+x = 18
c+d = 38
a
2 + h
2 = c
2
b
2 + h
2 = d
2
jak widzimy ... w obu przypadkach −−− mamy więcej niewiadomych niż równań ... związku z tym,
rozwiązanie będzie zależne od parametru (o którejś z niewiadomych
9 paź 23:44
wredulus_pospolitus:
dodatkowo − w obu przypadkach wiemy, że r ∊ (9,10)
9 paź 23:46
10 paź 00:18
a7: poprawiam y=10−198
10 paź 00:22
a7: y=10x−198
10 paź 00:22
a7: 19,8<x<20,2
10 paź 00:24
a7: dla x=19,8 r=
dla x=20,2 r=
odp. r∊(....., .....)

? może tak?
10 paź 00:28
wredulus_pospolitus:
skąd masz: y = 10x − 198

skąd to jest

10 paź 00:41
wredulus_pospolitus:
okey ... już wiem
10 paź 00:43
wredulus_pospolitus:
I @a7 −−− to jest tylko pierwszy przypadek trapezu ... jeszcze wersja a'la równoległobok

10 paź 00:46
a7: Ok
10 paź 00:55
an:
Raczej unikamy Herona, ale jak tu widać nie jest taki "straszny"
d=40−c
z Herona ( Brahmagupty)
P=
√22*18 *(40−c)*c
| | 2P | | √22*18*c*(40−c) | |
R= |
| = |
| |
| | a+b+c+d | | 40 | |
| | 198 | | 202 | |
Przy czym c musi się zawierać pomiędzy |
| ≤ c ≤ |
| co już wykazał a7 |
| | 10 | | 10 | |
| | 99 | |
tym samym R będzie się zawierało pomiędzy Rmin = |
| ⇒ Rmax=√99 |
| | 10 | |
12 paź 15:10
πqś:
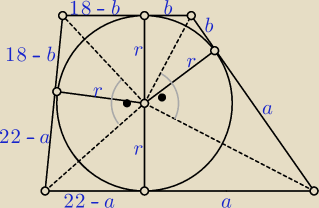
Szkic.
| | 9 | |
r2 = ab i r2 = (22 − a)(18 − b) ⇒ ab = 396 − 18a − 22b + ab ⇒ b = 18 − |
| a |
| | 11 | |
maksimum r
2 dla a = 11, wtedy trapez jest równoramienny i b = 9.
Dla a = 11 i b = 9: r
2 = 11*9 = 99 ⇒ r = 3
√11
12 paź 16:18
 a+b = 2
c+d = 18+20 = 38
a2 + h2 = c2
b2 + h2 = d2
a tak naprawdę to jest tylko jedna (mniej skomplikowana) z dwóch możliwości
a+b = 2
c+d = 18+20 = 38
a2 + h2 = c2
b2 + h2 = d2
a tak naprawdę to jest tylko jedna (mniej skomplikowana) z dwóch możliwości
 a+x = 20
b+x = 18
c+d = 38
a2 + h2 = c2
b2 + h2 = d2
jak widzimy ... w obu przypadkach −−− mamy więcej niewiadomych niż równań ... związku z tym,
rozwiązanie będzie zależne od parametru (o którejś z niewiadomych
a+x = 20
b+x = 18
c+d = 38
a2 + h2 = c2
b2 + h2 = d2
jak widzimy ... w obu przypadkach −−− mamy więcej niewiadomych niż równań ... związku z tym,
rozwiązanie będzie zależne od parametru (o którejś z niewiadomych
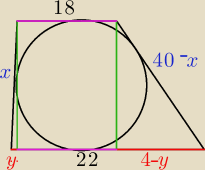 https://matematykaszkolna.pl/strona/874.html
r=2P/(80)
z tw. Pitagorasa x2=y2+4r2 i (40−x)2=(4−y)2+4r2
y=10x−2 6−10x>0 ⇒ x<0,6 ⇒ 2r<0,6 ⇒ sprzeczne
https://matematykaszkolna.pl/strona/874.html
r=2P/(80)
z tw. Pitagorasa x2=y2+4r2 i (40−x)2=(4−y)2+4r2
y=10x−2 6−10x>0 ⇒ x<0,6 ⇒ 2r<0,6 ⇒ sprzeczne
 nie istnieje taki trapez gdyż 18<2r<22
nie istnieje taki trapez gdyż 18<2r<22
 ? może tak?
? może tak?
 skąd to jest
skąd to jest 

 Szkic.
Szkic.