pole
Mik: Niech ABCD będzie czworokątem wypukłym z AB=5, AD=17 i CD=6. Jeśli dwusieczne kątów BAD i ADC
przecinają się w środku BC, oblicz pole ABCD.
22 wrz 10:55
a7:
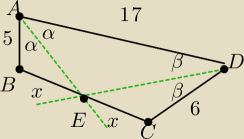
22 wrz 13:49
Mik: A jak policzyc pole?
22 wrz 16:09
Mila:
Masz jakąś odpowiedź?
22 wrz 19:04
Mila:
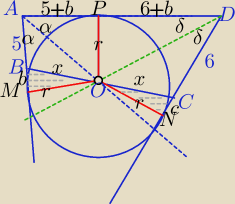
1)
ΔBOM≡ΔCON −Δ prostokątne
b=c
5+b+6+b=17
2b=6 ⇔b=c=3
2)
r=?
Na razie tyle mam.
22 wrz 19:06
Mik: nie mam odpowiedzi
22 wrz 19:36
Mila:
Otrzymałam (nie podobają mi się rachunki): sin(2α)=1, wtedy r=8 ?
Znajdę inne zależności. A7 −pomocy!
22 wrz 21:07
Mariusz:
Z rysunku Mili wynika że czworokąt AMOP
można podzielić na dwa trójkąty równoramienne
22 wrz 21:54
Mila:
Mam. Napiszę.
22 wrz 22:04
A7:
r=√21
23 wrz 12:13
Mik: Jak to rozwiazac
23 wrz 13:42
Mariusz:
Dodatkowo nie widać z jakiego kryterium Mila skorzystała aby pokazać że trójkąty BOM i COM
są przystające
Mamy równość długości dwóch par boków oraz równość miar jednej pary kątów
(to widać od razu) a chcemy pokazać równość długości trzeciej pary boków
Tylko że ten kąt prosty nie pasuje do kryterium z dwoma bokami
a nie wystarczy do kryterium z jednym bokiem
23 wrz 13:56
A7:
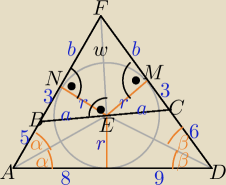
| | r2 | |
Z podobieństwa trójkątów ECM i EMF: b = |
| |
| | 3 | |
| | 1 | |
p = |
| (|AD| + |DF| + |AF|) połowa obwodu trójkąta ADF |
| | 2 | |
pole trójkąta ADF: pr = (wzór Herona) stąd r
2 = 21
23 wrz 14:47
Mariusz:
A7 Z rysunku nie widać z jakiego kryterium korzystasz
aby stwierdzić że trójkąty są podobne np równości miar kątów
(widać tylko że obydwa trójkąty są prostokątne)
Korzystasz z wyników Mili a ona też nie podała kryterium przystawania
23 wrz 15:13
A7:
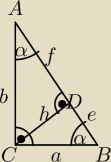
Kto bystry, to dostrzeże na rysunku potrzebne informacje. Nie chciałem wyjaśniać każdego kroku.
Skorzystałem z obliczeń wcześniej tu przedstawionych.
| | e | | h | | h2 | |
Szkoła podstawowa: ΔBCD ∼ ΔCDA ⇒ |
| = |
| ⇒ f = |
| |
| | h | | f | | e | |
23 wrz 15:24
Mariusz:
No właśnie chodziło o uzasadnienie tych równości miar kątów zaznaczonych
na rysunku z wpisu 23 wrz 2022 15:24 jako α
23 wrz 15:42
Mila:
Miło A7 za włączenie się do problemu.

W poprzednich obliczeniach mam błąd, stąd błędny wynik
r=8.
Licząc kilka razy uzyskałam wynik różny od poprzedniego (taki jak u Ciebie).
23 wrz 15:51
Mariusz:
Nadal nie pokazujecie kryteriów z których korzystacie
Mila − trójkąty przystające , A7 − trójkąty podobne
Poza tym mam wątpliwości czy we wpisie z 23 wrz 2022 15:24
poprawnie oznaczył kąty bo z jego rysunku wynika że a=b
a tak nie musi być
23 wrz 16:07
Mariusz:
W trójkątach ΔFEC , ΔMEC , ΔFEM
mamy raczej taką samą sytuację jak przy dowodzeniu twierdzenia Pitagorasa
i niekoniecznie musi być to zgodne z rysunkiem z 23 wrz 2022 15:24
23 wrz 16:13
Mila:
Mariusz
Przystawanie trójkątów prostokątnych.
Jeżeli w dwóch trójkątach prostokątnych dwa boki jednego trójkąta są odpowiednio równe
dwóm bokom drugiego trójkąta, a kąt prosty w jednym trójkącie jest położony względem tych boków
tak samo,
jak w drugim trójkącie, to trójkąty te są przystające.
23 wrz 16:18
Mila:
A7 oczywiście − dziękuję

.
23 wrz 16:19
Mariusz:
Jak się przeliczy miary kątów to widać równość miar kątów i dostaniemy podobieństwo trójkątów
a co z tym wcześniejszym przystawaniem
Mamy równość długości dwóch par boków (x oraz r na rysunku Mili)
oraz równość miar jednej pary kątów
(to widać od razu) a chcemy pokazać równość długości trzeciej pary boków
Tylko że ten kąt prosty nie pasuje do kryterium z dwoma bokami
a nie wystarczy do kryterium z jednym bokiem
23 wrz 16:23
a7: kim jest A7?
23 wrz 16:26
a7: czy to Eta?
23 wrz 16:26
Mariusz:
Mila a to ja znam z kątem między dwoma bokami
i z kątami przy jednym danym boku
No to razem rozwiązaliście to zadanie
23 wrz 16:27
a7: hmmmm, nie widzę (po rysunkach), że to nie Eta
23 wrz 16:27
a7: no nic kimkolwiek jest A7 pozdrawiam
23 wrz 16:27
Mariusz:
A7 przedstawia się jako mężczyzna więc wątpię
(Tak w języku polskim można to stwierdzić po odmianie
i między innymi dlatego uważam angielski za prymitywny)
23 wrz 16:33
Mila:
Galimatias

23 wrz 16:38
Mariusz:
Przez chwilę pomyślałem o tym przedłużeniu boków aby otrzymać trójkąt z okręgiem wpisanym
i porównać wzory na pole powierzchni tego trójkąta
jednak w chwili gdy o tym pomyślałem nie miałem pomysłu na długości boków trójkąta
Po wtóre za bardzo skupiłem się na pomyśle który do niczego nie prowadził
Tak więc rozwiązanie było w moim zasięgu bo gdybym skorzystał z tego pomysłu którego
odrzuciłem to pewnie bym znalazł to podobieństwo trójkątów
Mila a ta cecha przystawania trójkątów o której wspominałaś da się sprowadzić do cechy dla
dowolnego trójkąta
Zadanie jest już rozwiązane ale ciekaw jestem twojego sposobu rozwiązania
(tam gdzie nie podobały ci się rachunki i wyszedł błędny wynik)
23 wrz 16:53
Mila:
Mogę podać mój pierwszy sposób, też wychodzi tyle samo. Jednak skorzystałam
później z wzoru Herona, bo ładnie się liczyło.
23 wrz 17:30
Mila:
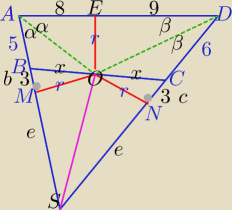
1)
| | 1 | |
PABCD= |
| *r*(17+6+5)=14r |
| | 2 | |
2)
ΔBOM≡ΔCON −Δ prostokątne
b=c
5+b+6+b=17
2b=6 ⇔b=c=3
| | r | | 8 | |
3) sinα= |
| , cosα= |
| |
| | |AO| | | |AO| | |
| | 8r | |
sinα*cosα= |
| , |AO|2=r2+64 |
| | |AO|2 | |
4) ΔBCS− Δrównoramienny, dwusieczna kąta S jest wysokością opuszczoną na BC
r
2=3*e, r=
√3e
5)
| | 1 | | 1 | | 16√3e | |
PΔADS= |
| *17*(8+e)*sin2α= |
| *17*(8+e)* |
| |
| | 2 | | 2 | | 3e+64 | |
| | 17*8*(8+e)√3e | |
(*) PΔADS= |
| |
| | 3e+64 | |
lub
(**)P
ΔADS=p*r=(17+e)*
√3e
Porównanie pól:
| 17*8*(8+e)√3e | |
| =(17+e)*√3e |
| 3e+64 | |
136*(8+e)=(17+e)*(3e+64)
stad e=7
r
2=3*7=21
r=
√21
===================
Jeżeli zastosujesz zamiast wzoru (*) wzór Herona na pole to masz:
P
ΔADS=
√(17+e)*(17+e−17)*(17+e−8−e)*(17+e−9−e)
P
ΔADS=
√(17+e)*e*9*8
Porównanie z (**)
√72*(17+e)*e=(17+e)*
√3e, e>0
21e=3e
2
3e=21, r
2=21
===========
23 wrz 18:14
Mariusz:
r2=3*e to z trójkątów podobnych
Sytuacja taka jak u A7
I to był twój pierwszy pomysł bo wyglądało na to że najpierw liczyłaś sin(2α)
a potem dopiero r
23 wrz 18:43
Mila:
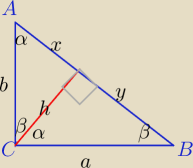
Twierdzenie:
W trójkącie prostokątnym kwadrat wysokości poprowadzonej z wierzchołka kąta prostego
jest równy iloczynowi długości odcinków, na które ta wysokość podzieliła przeciwprostokątną.
h
2=x*y
Dowód z podobieństwa trójkątów
23 wrz 18:50
Mila:
Wyrażałam sin2α za pomocą odpowiednich odcinków, aby zastosować do obliczenia pola ΔADS,
potem porównać z innym wzorem na pole w celu wyznaczenia wartości e od której uzależniłam r.
23 wrz 18:54
A7:

dla Ety
23 wrz 19:20
Mariusz:
Zostałeś z nią pomylony
23 wrz 20:20
a7: nic ja tylko na wszelki wypadek dopowiem raz jeszcze ja jestem kim innym niż A7, ale to
chyba celowy galimatias
23 wrz 20:29
Mariusz:
A co odnosisz wrażenie że Mila cię z nim pomyliła
Dziwne bo chyba widzi nasz numer IP
23 wrz 21:02
25 wrz 00:09
a7: 
27 wrz 18:49

 1)
1)

 Kto bystry, to dostrzeże na rysunku potrzebne informacje. Nie chciałem wyjaśniać każdego kroku.
Skorzystałem z obliczeń wcześniej tu przedstawionych.
Kto bystry, to dostrzeże na rysunku potrzebne informacje. Nie chciałem wyjaśniać każdego kroku.
Skorzystałem z obliczeń wcześniej tu przedstawionych.
 W poprzednich obliczeniach mam błąd, stąd błędny wynik
r=8.
Licząc kilka razy uzyskałam wynik różny od poprzedniego (taki jak u Ciebie).
W poprzednich obliczeniach mam błąd, stąd błędny wynik
r=8.
Licząc kilka razy uzyskałam wynik różny od poprzedniego (taki jak u Ciebie).
 .
.

 1)
1)
 Twierdzenie:
W trójkącie prostokątnym kwadrat wysokości poprowadzonej z wierzchołka kąta prostego
jest równy iloczynowi długości odcinków, na które ta wysokość podzieliła przeciwprostokątną.
h2=x*y
Dowód z podobieństwa trójkątów
Twierdzenie:
W trójkącie prostokątnym kwadrat wysokości poprowadzonej z wierzchołka kąta prostego
jest równy iloczynowi długości odcinków, na które ta wysokość podzieliła przeciwprostokątną.
h2=x*y
Dowód z podobieństwa trójkątów
 dla Ety
dla Ety
 https://matematykaszkolna.pl/forum/414336.html
i pozdrawiam a7
https://matematykaszkolna.pl/forum/414336.html
i pozdrawiam a7
